Determine the average power delivered to each of the three boxed networks in the circuit of Fig..
Z1 = 6 − j8 = 10 ∠−53°13° ; Z2 = 2 + j14 = 14.14 ∠ 81.87° ; Z3 = 6 − j8 = 10 ∠ − 53.13°Z23 = Z2Z3/Z2 + Z3 = 14.14 ∠ - 8.13° = 14 - j2Drop across two parallel impedances is given byV23 = 10014 - j2/6 - j8 + 14 - j2 = 63.2∠18.43° = 60 + j20V1 =10010 ∠ - 53.13°/6 - j8 + 14 - j2 = 47.7 ∠ -26.57° = 40 - j20I1 = 44.7 ∠- 26.57°/10 ∠- 53.13° = 4.47 ∠26.56°I2 = 63.2 ∠-18.43°/14.14 ∠ 81.87° = 4.47 ∠ - 63.44°I3 = 63.2 ∠ 18.43°/10 ∠ - 53.13° = 6.32 ∠ 71.56°P1 = V1I1 cos φ1 = 44.7 × 4.47 × cos 53.13° = 120 W P2 = V2 I2 cos φ2 = 63.2 × 4.47 × cos 81.87° = 40 W; P3 = V3I3 cos φ3 = 63.2 × 6.32 × cos 53.13° = 240 W Total = 400 WAs a check power delivered by the 100-V source is P = VI1 cos φ = 100 × 4.47 × cos 26.56° = 400 W
Related Solutions
In the circuit shown the cell will deliver maximum power to the network if the value of R is
View SolutionIn the circuit shown the cell will deliver maximum power to the network if the value of R is
View SolutionDetermine the current in each branch of the network shown in Fig.
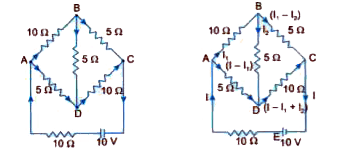
View SolutionDetermine the current in each branch of the network shown in fig.
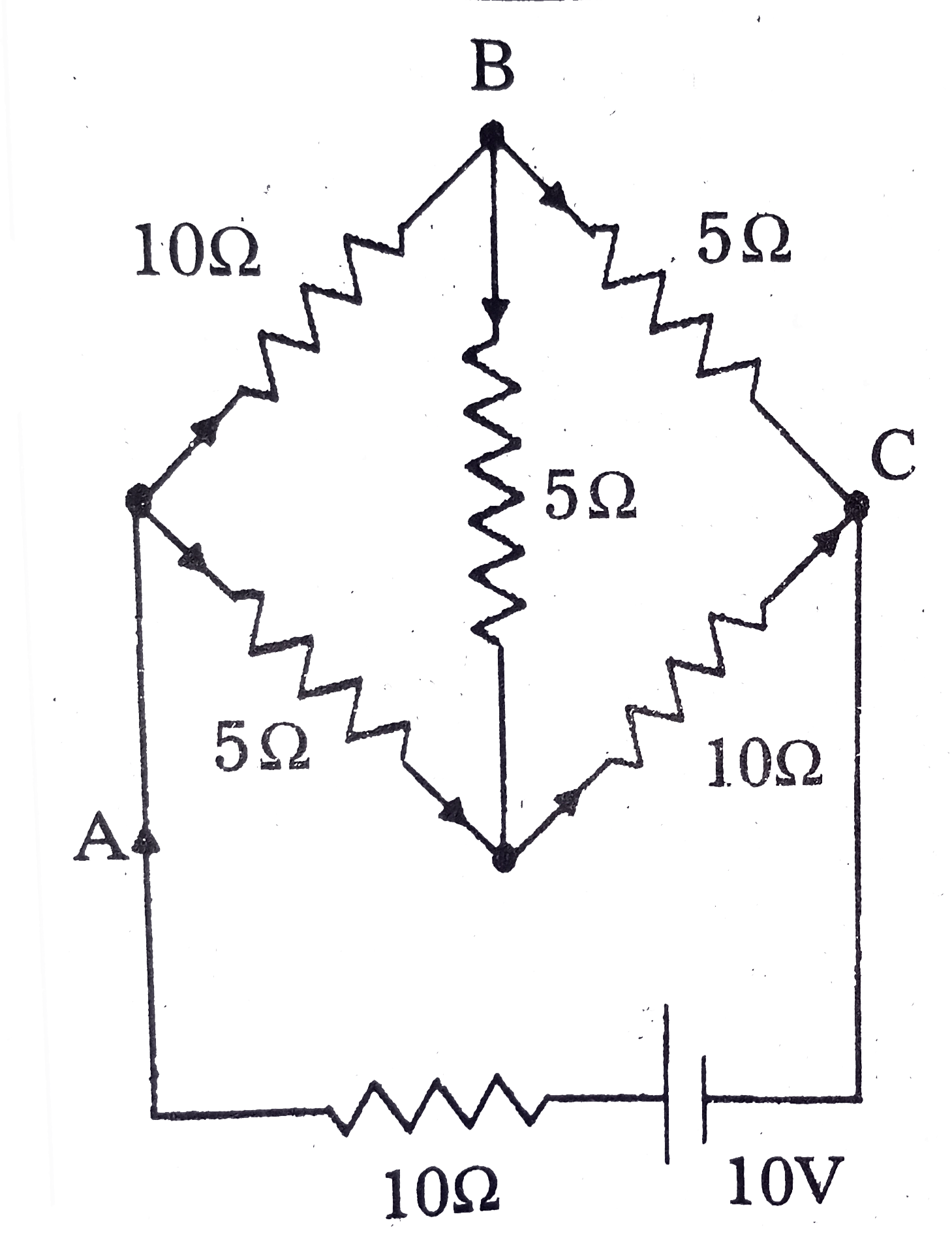
View SolutionDetermine the current in each branch of the network shown in Fig.
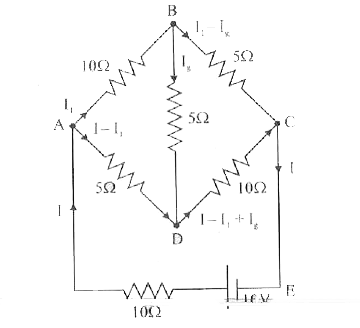
View SolutionDetermine the current in each branch of the network shown in fig.
View SolutionDetermine the current in each branch of the network shown in fig.
View Solution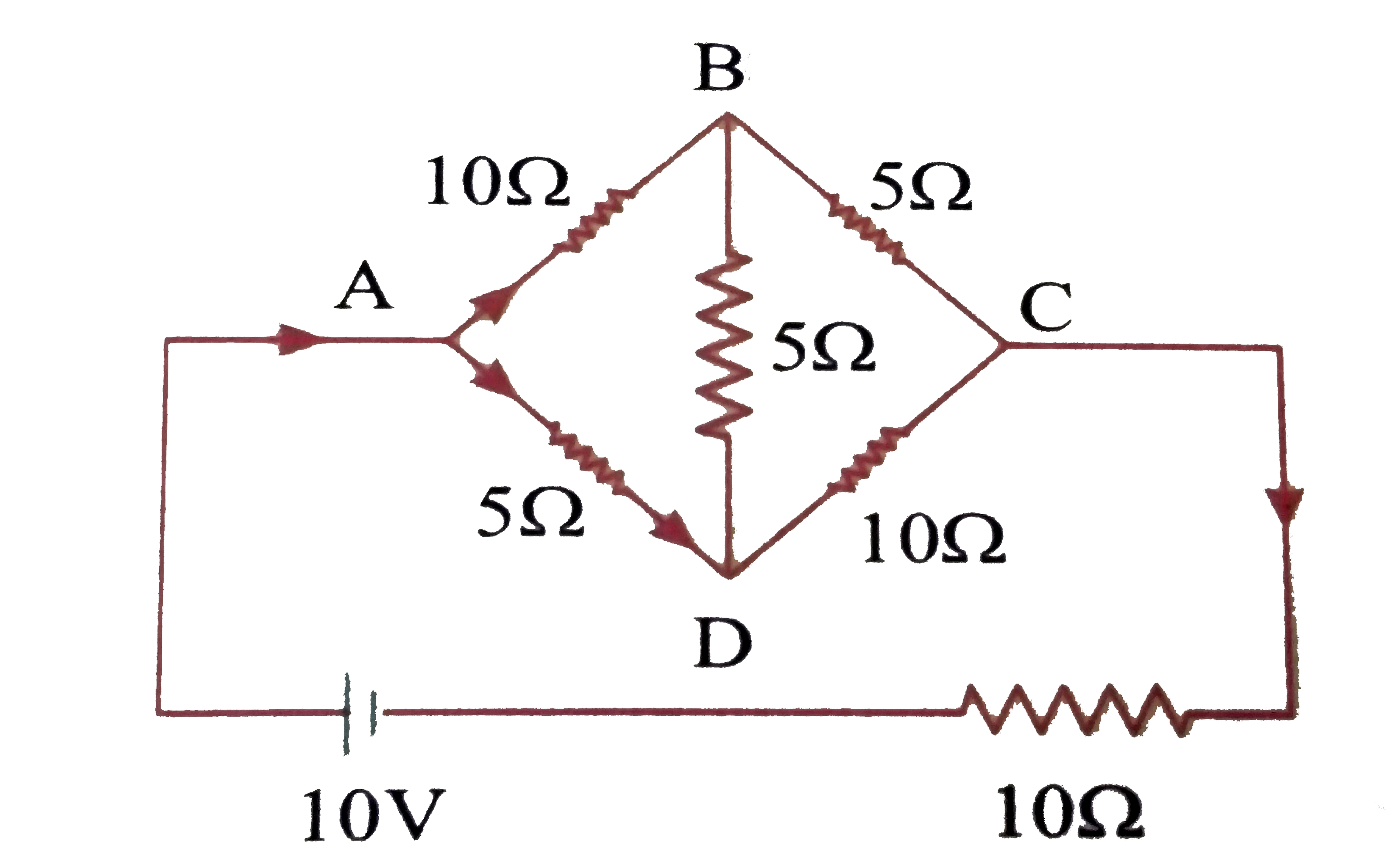
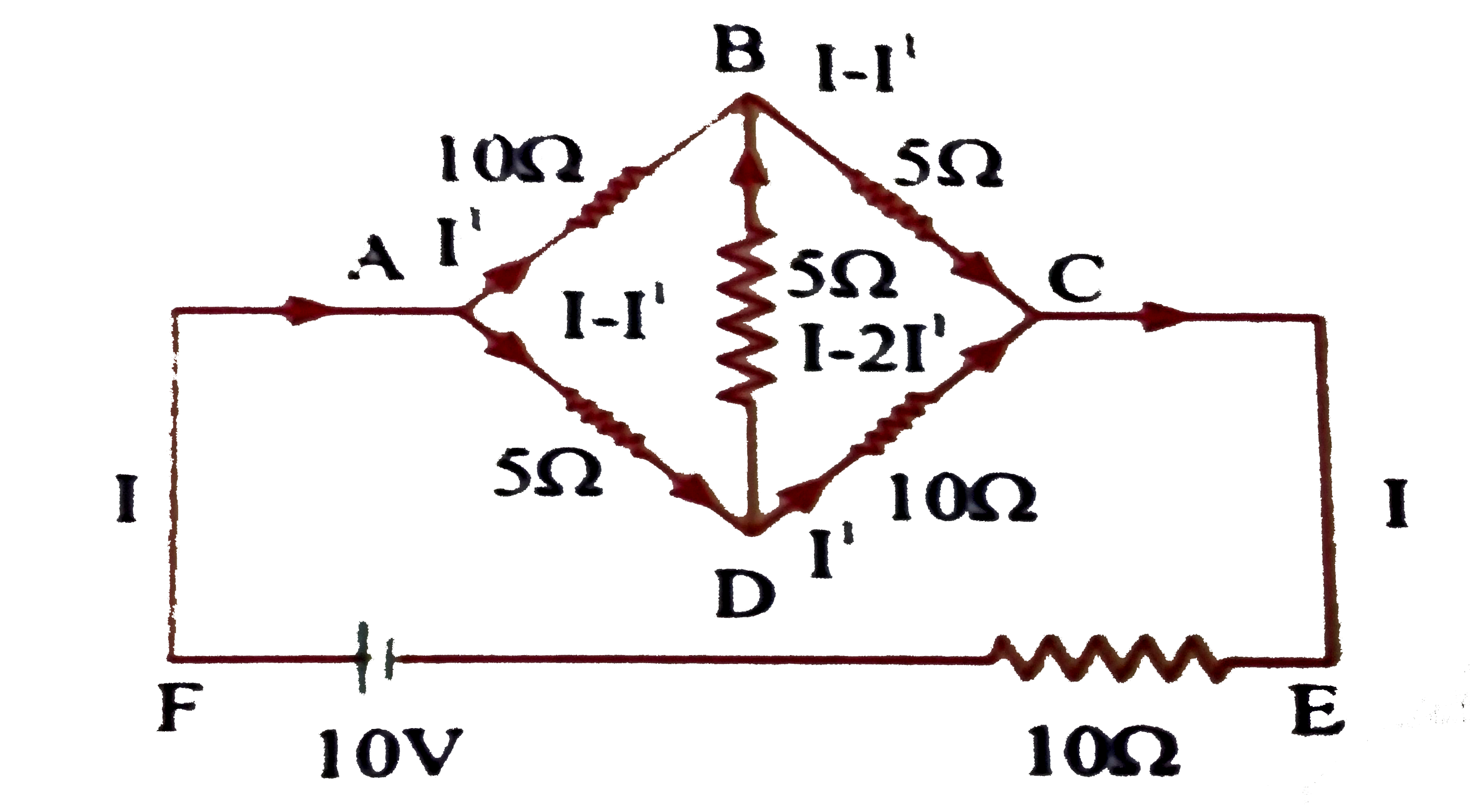
Determine the current in each branch of the network shown in fig.
View SolutionDetermine the current in each branch of the network shown in Fig.
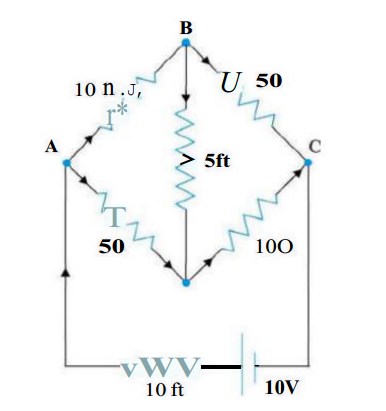
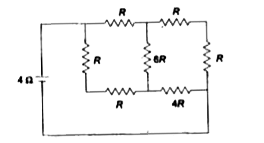
View SolutionA battery of internal resistance 4 is connected to the network or resistances as shown in Fig. In order that maximum power cab be delivered to the network, the value of R in ohm should be
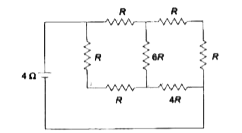
View SolutionA battery of internal resistance is connected to the network of resistances as shown in the fig. In order that the maximum power can be delivered to the network, the value of R in should be
View SolutionA battery of internal resistance 4Omega is connected to the network of resistances as shown in the fig. In order that the maximum power can be delivered to the network, the value of R in Omega should be
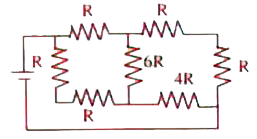
View SolutionA battery of internal resistance is connected to the network of resistances as shown in Fig. In order that maximum power can be delivered to the network, the value of R in ohm should be:
View SolutionDetermine the current in each branch of the network shown in Fig. 3.24

View SolutionDetermine the load resistance for which the power delivered to the circuit is a maximum. Graph the dependence of the power on the load resistance.
View SolutionDetermine the load resistance for which the power delivered to the circuit is a maximum. Graph the dependence of the power on the load resistance.
View SolutionThe plot given below is of the average power delivered to an LRC circuit versus frequency. Resistance of circuit is 100 12. Capacitive reactance of circuit at resonance (in (2) is 1.0 average power (microwatts) 0.5 0.0 frequency (kHz)
View SolutionDetermine the equivalent resistance of networks shown in Fig. 3.31. :
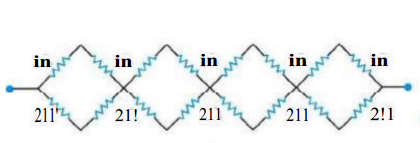
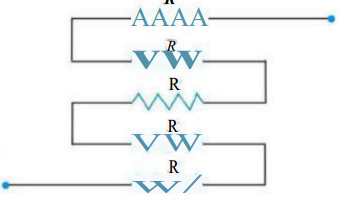
View SolutionDetermine the equivalent resistance of networks shown in Fig.

View Solution[" The plot given below is of the "],[" average power delivered to an "],[" LRC circuit versus frequency."],[" Resistance of circuit is "100Omega" ."],[" Capacitive reactance of circuit at "],[" resonance (in "Omega" ) is "]
View Solution