Analyse the motion of two bodies connected by a string when one body is lying on a horizontal surface and other is hanging free for the following cases. 1. The horizontal surface is smooth and the string is passing over a smooth pulley. 2. The horizontal surface is rough and string is passing over a smooth pulley. 3. The horizontal surface is rough and string is passing over a rough pulley.
CASE-1: THE HORIZONTAL SURFACE IS SMOOTH AND THE STRING IS PASSING OVER A SMOOTH PULLEY: Figa shows the two weights W1 and W2 connected by a light inextensible string passing over a smooth pulley. The weight W2 is placed on a smooth horizontal surface whereas the weight W1 is hanging free.The weight W1 is moving downwards whereas the weight W2 is moving on smooth horizontal surface. The velocity and acceleration of W1 will be same as that of W2. As the string is light and inextensible and passing over a smooth pulley the tensions of the string will be same on both sides of the pulley.For W1 block: Move downW1 – T = W1/g.a .....1For W2 blockSince W act vertically and T act Horizontally & w.cos 90 = 0 Solve both the equation for the value of ‘T’ and ‘a’.CASE-2: THE HORIZONTAL SURFACE IS ROUGH AND STRING IS PASSING OVER A SMOOTH PULLEY.Figb shows the two weights W1 and W2 connected by a light inextensible string passing over a smooth pulley. The weight W2 is placed on a rough horizontal surface whereas the weight W1 is hanging free. Hence in this case force of friction will be acting on the weight W2 in the opposite direction of the motion of weight W2.Let µ = Coefficient of friction between weight W2 and horizontal surface. Force of friction = µR2 = µW2.Motion of W1 Down Motion W1 – T = W1/g.a ...1Motion of W2 T – µ.W2 = W2/g.a ...2 Solve the equations for Tension ‘T’ and Acceleration ‘a’CASE-3: THE HORIZONTAL SURFACE IS ROUGH AND STRING IS PASSING OVER A ROUGH PULLEY. Figc shows the two weights W1 and W2 connected by a string passing over a rough pulley. The weight W2 is placed on a rough horizontal surface whereas the weight W1 is hanging free. Hence in this case force of friction will be acting on the weight W2 in the opposite direction of the motion. As the string is passing over a rough pulley. The tension on both side of the string will not be same. Let µ1 = Coefficient of Friction between Weight W2 and Horizontal plane µ2 = Coefficient of Friction between String and pulley T1 = Tension in the string to which weight W1 is attached.T2 = Tension in the string to which weight W2 is attachedForce of friction = µ1R2 = µ1W2Consider block W1 W1 – T1 = W1/g.a ...1Consider block W2T2 – µ2.W2 = W2/g.a ...2 Another equation is T1/T2 = eµ.θ ...3 Solve all three equation for the value of ‘a’ ‘T1’ and ’T2’
Related Solutions
A block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string passing over a smooth pulley. The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
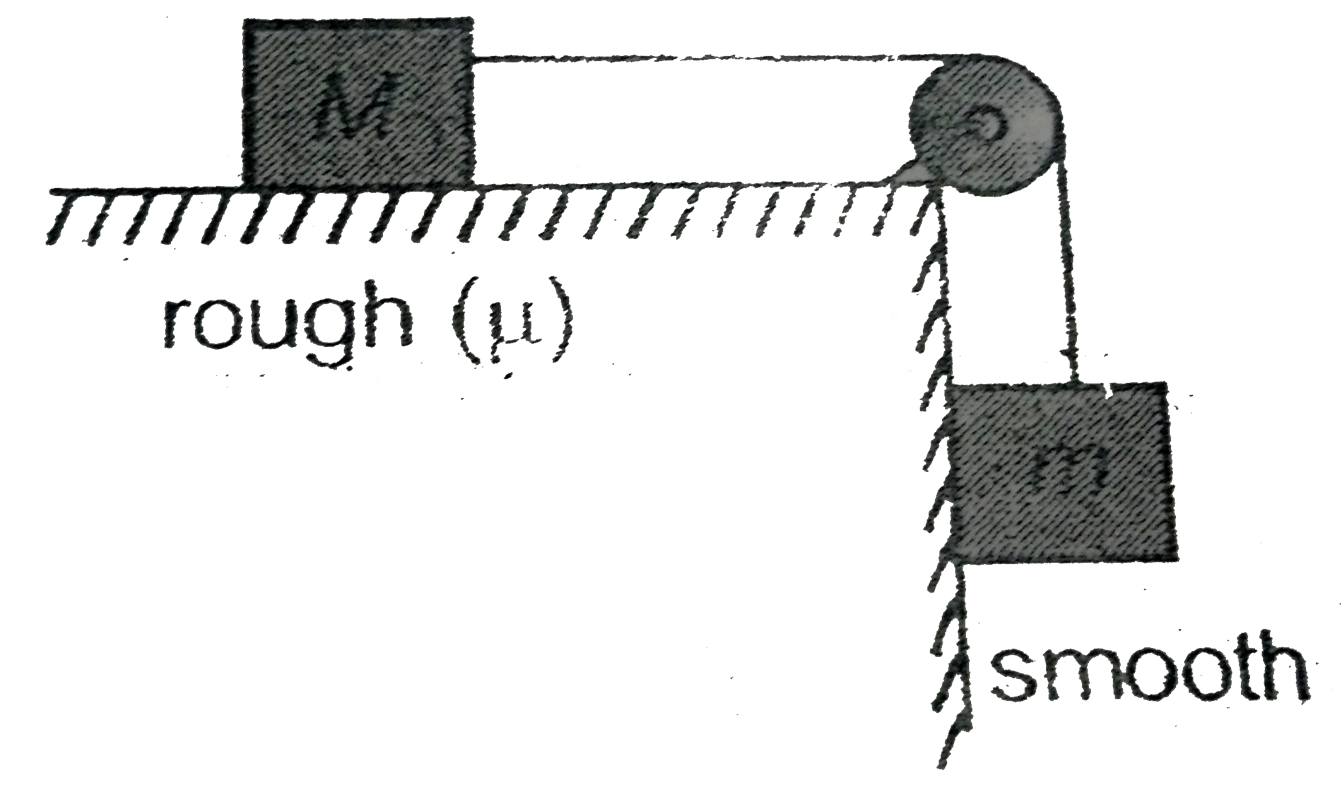
If the whole system ( horizontal surface + blocks ) accelerates towards right the value of maximum on the horizontal surface is
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string passing over a smooth pulley. The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m

If the whole system ( horizontal surface + blocks ) accelerates towards right the value of maximum on the horizontal surface is
View SolutionPulleys and strings are massless. The horizontal surface is smooth. What is the acceleration of the block
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
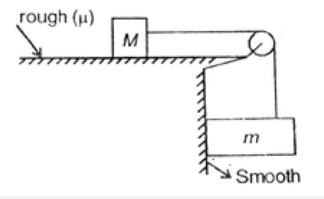
The minimum value of coefficient of friction such that system remains at rest , is
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m The minimum value of coefficient of friction mu such that system remains at rest , is
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string passing over a smooth pulley. The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m If the coefficient of friction of friction mu is less than the above value, then downward acceleration of block m is
View SolutionTwo blocks are connected by an inextensible light string, the string is passing over smooth, light pulley as shown. Find the acceleration of blocks and tension in the string, reaction in pulley.
View SolutionTwo bodies of masses 6 kg and 4 kg respectively are connected to two ends of a light string passing over horizontal frictionless pulley. The acceleration in the string is :
View SolutionTwo masses ,each equal to m ,are arrached to one another by a massless string passing over a smooth pulley the tension in the string is :
View SolutionIn the figure shown,assuming the horizontal surface to be smooth and (g=10ms^(-2)) ,if the pulleys and the strings connecting are ideal,then acceleration of the block (3.0Kg)" is
View SolutionTwo bodies of masses 4kg and 3kg respectively are connected by a light string passing over a smooth frictionless pulley Calculate the acceleration of the masses and tension in the string .
View SolutionLower surface of a plank is rough and lying at rest on a rough horizontal surface. Upper surface of the plank is smooth and has a smooth hemisphere placed over it through a light string as shown in the figure. After the string is burnt, trajectory of C.M , of the sphere is
View SolutionLower surface of a plank is rough and lying at rest on a rough horizontal surface. Upper surface of the plank is smooth and has a smooth hemisphere placed over it through a light string as shown in the figure. After the string is burnt, trajectory of C.M , of the sphere is
View SolutionA book of mass 5 kg is kept on a horizontal table. It is connected to a weight of mass 2 kg by a weightless string passing over a smooth pulley . The part of the string on the table is horizontal, and the weight is hanging freely from the pulley. If the coefficient of kinetic friction between the table and the block is 0.2, find the acceleration of the block. What will be the tension in the string ?
View SolutionTwo bodies of mass M and m are tied at the ends of a string. The string passes over a smooth pulley and both the bodies hang in an upright position at its ends. Find the common acceleration of both the bodies and the tension of the string.
View SolutionTwo blocks of masses 2 kg and 4 kg are connected by a light string passing over a light smooth pulley clamped to the edge of a horizontal table. The 2 kg block is on the smooth horizontal table and the other block is hanging vertically. (i) Find the acceleration of the stem if it is released from rest. (ii) Find the tension in the string.
View SolutionTwo blocks of masses 2 kg and 4 kg are connected by a light string passing over a light smooth pulley clamped to the edge of a horizontal table. The 2 kg block is on the smooth horizontal table and the other block is hanging vertically, (i) Find the acceleration of the stem if it is released from rest, (ii) Find the tension in the string.
View SolutionTwo blocks of masses 2 kg and 4 kg are connected by a light string passing over a light smooth pulley clamped to the edge of a horizontal table. The 2 kg block is on the smooth horizontal table and the other block is hanging vertically, (i) Find the acceleration of the stem if it is released from rest, (ii) Find the tension in the string.
View SolutionTwo blocks of masses 2 kg and 4 kg are connected by a light string passing over a light smooth pulley clamped to the edge of a horizontal table. The 2 kg block is on the smooth horizontal table and the other block is hanging vertically. (i) Find the acceleration of the stem if it is released from rest. (ii) Find the tension in the string.
View SolutionTwo masses kg and kg passes over a pulley. Find the ratio of the masses so that string passes over the pulley will just start slipping over is surface. The friction coefficient between the string and pulley surface is 0.2
View Solution