A system of weight connected by string passing over pulleys A and B is shown in fig. Find the acceleration of the three weights. Assume weightless string and ideal condition for pulleys.
As the strings are weightless and ideal conditions prevail hence the tensions in the string passing over pulley A will be same. The tensions in the string passing over pulley B will also be same. But the tensions in the strings passing over pulley A and over pulley B will be different as shown in fig. Let T1 = Tension in the string passing over pulley A T2 = Tension in the string passing over pulley B One end of the string passing over pulley A is connected to a weight 15N and the other end is connected to pulley B. As the weight 15N is more than the weights 6 + 4 = 10N hence weight 15N will move downwards whereas pulley B will move upwards. The acceleration of the weight 15N and of the pulley B will be same. Let a = Acceleration of block 15N in downward directiona 1 = Acceleration of 6N downward with respect to pulley B. Then acceleration of weight of 4N with respect to pulley B = a1 in the upward direction.Absolute acceleration of weight 4N = Acceleration of 4N w.r.t. pulley B + Acceleration of pulley B.= a1 + a upwardas both acceleration are in upward direction total acceleration will be sum of the two accelerations Absolute acceleration of weight 6N = Acceleration of 6 w.r.t. pulley B + Acceleration of pulley B. = a1 – a downwardAs a1 is acting downward whereas a is acting upward. Hence total acceleration in the downward directionConsider the motion of weight 15NNet downward force = 15 – T1Using F = ma 15 – T1 = 15/9.81a ...1 Consider the motion of weight 4N Net downward force = T2 - 4 Using F = ma T2 – 4 = 4/9.81a + a1 ...2 Consider the motion of weight 6N Net downward force = 6 - T2 Using F = ma 6 – T2 = 6/9.81a1 – a ...3 Consider the motion of pulley B T1 = 2T2 ...4 Adding equation 2 and 3 2 = 4/9.81a + a1 + 6/9.81a1 – a 9.81 = 5a1 – a ...5 Multiply equation 2 by 2 and put the value of equation 4 we getT1 – 8 = 8/9.81a1 + a ...6Adding equation 1 and 6 we get15 – 8 = 15/9.81a + 8/9.81a1 + a23a + 8a1 = 7 X 9.81 ...7Multiply equation 5 by 23 and add with equation 7 we get a1 = 2.39m/sec2Putting the value of a1 in equation 5 we get a = 2.15m/sec2 Acceleration of weight 15N = a = 2.15m/sec2Acceleration of weight 6N = a = 0.24m/sec2 Acceleration of weight 4N = a = 4.54m/sec2
Related Solutions
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.

View SolutionThree weights are hanging over a smooth fixed pulley as shown in the figure. What is the tension in the string connecting weights and ?
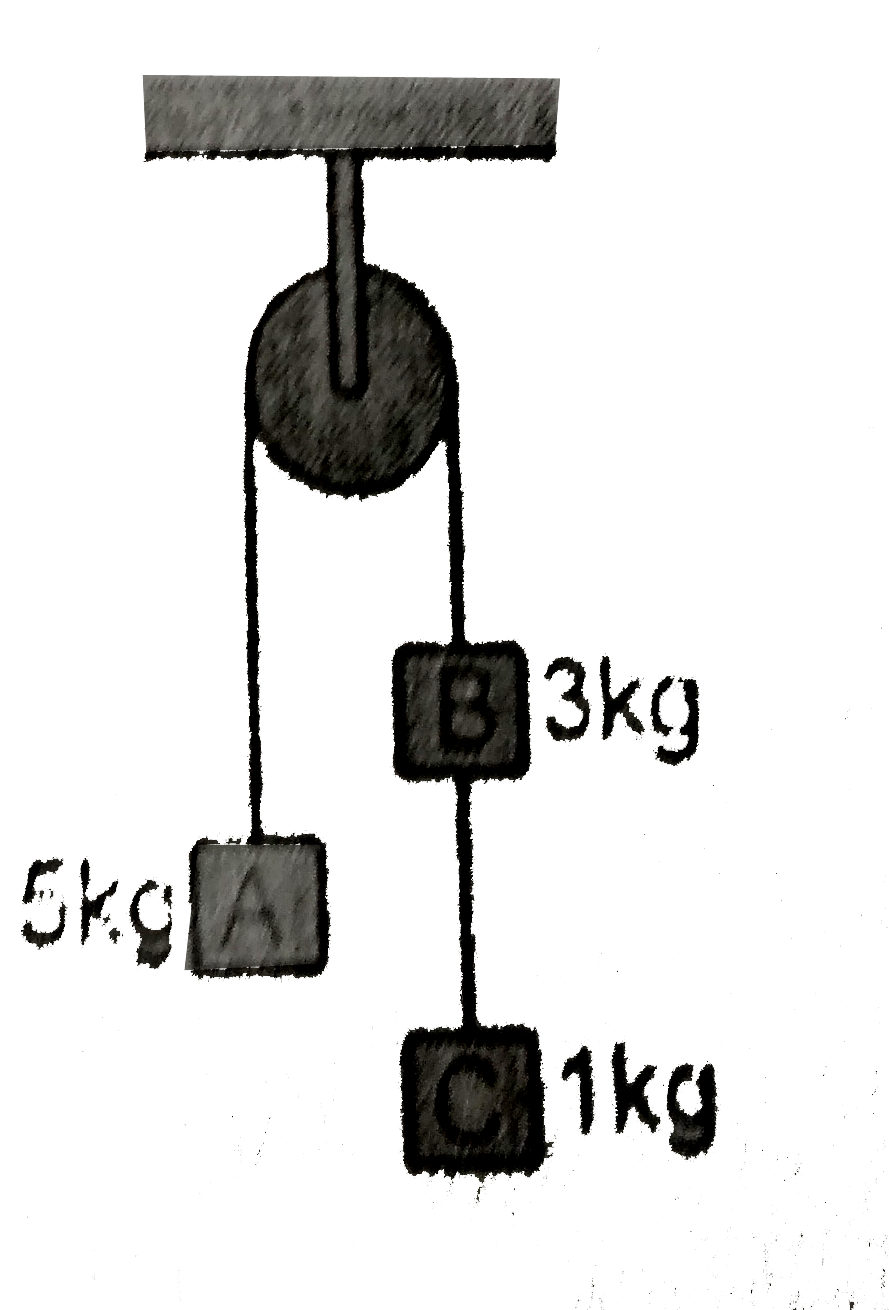
View SolutionThree weights are hanging over a smooth fixed pulley as shown in the figure. What is the tension in the string connecting weights and ?
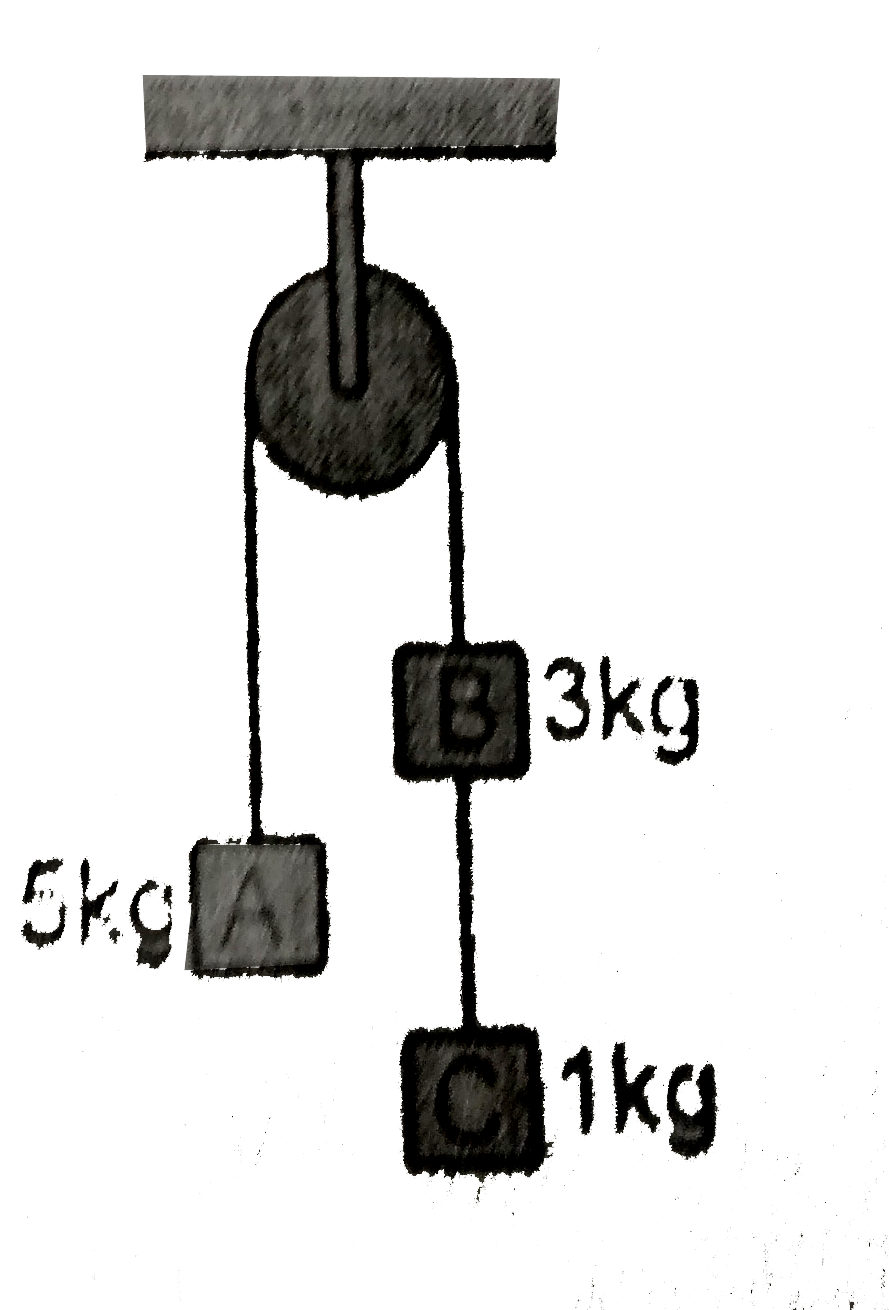
View SolutionThree equal weights of mass m each are hanging on a string passing over a fixed pulley as shown in fig. The tensions in the string connecting weights A to B and B to C will respectively be -
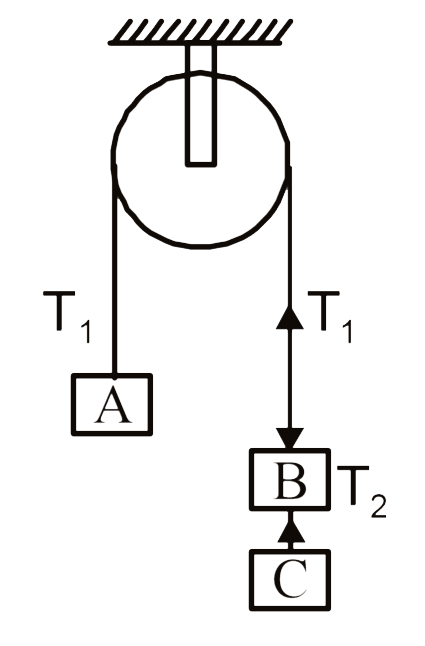
View SolutionThree equal weights of mass m each are hanging on a string passing over a fixed pulley as shown in Fig. What are the tensions in the string connecting weights A to B and B to C?
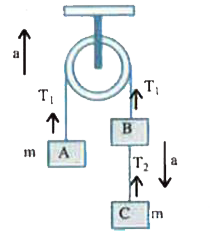
View SolutionThree equal weights of mass m each are hanging on a string passing over a fixed pulley as shown In Fig . What are the tensions in the string connecting weights A to B and B to C ?
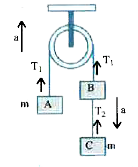
View SolutionThree equal weights of mass m each are hanging on a string passing over a fixed pulley as shown in Fig. What are the tensions in the string connecting weights A to B and B to C?
View SolutionThree equal weights of mass m each are hanging on a string passing over a fixed pulley as shown in Fig. What are the tensions in the string connecting weights A to B and B to C?
View SolutionThree equal weights of mass 2 kg each are hanging on a string passing over a fixed pulley as shown in fig What is the tension in the string connecting weights B and C?
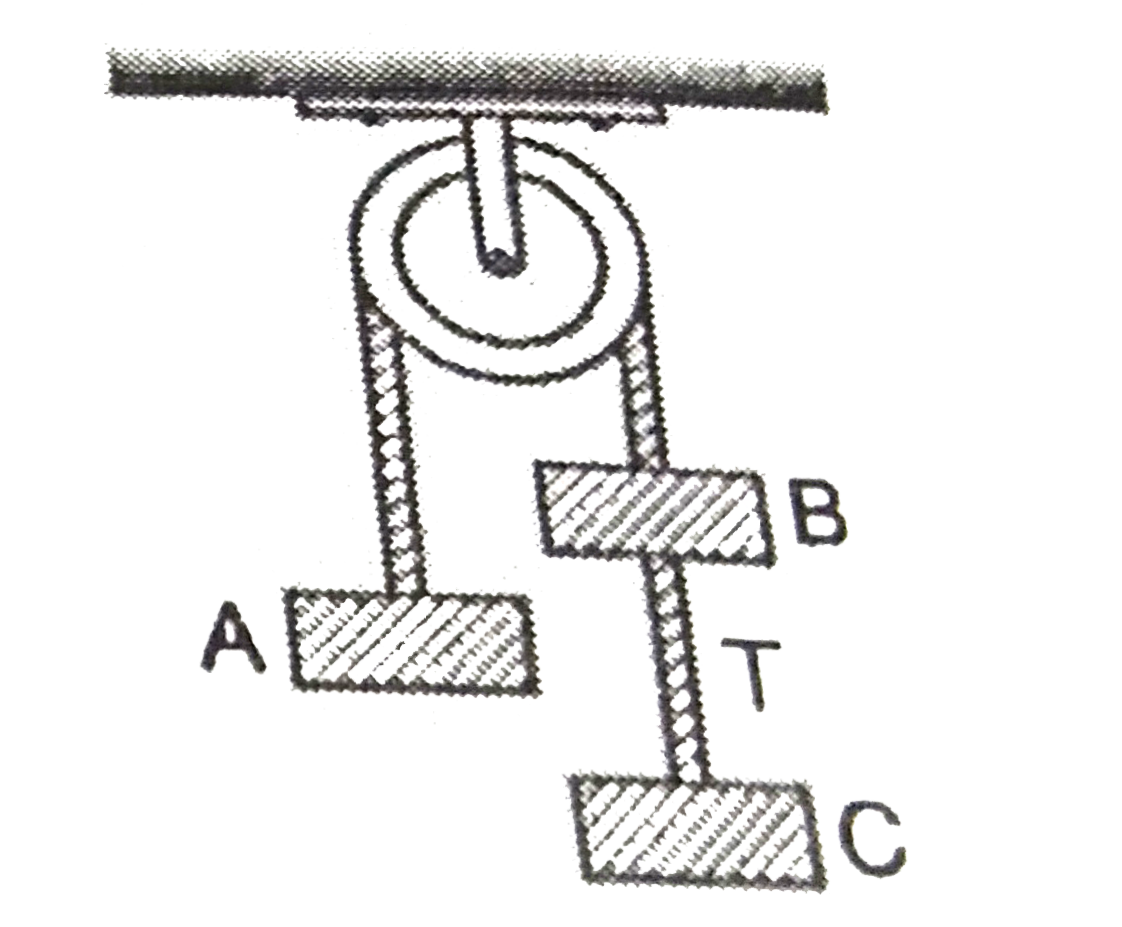
View SolutionThree equal weights of mass 2 kg each are hanging on a string passing over a fixed pulley as shown in fig What is the tension in the string connecting weights B and C?

View SolutionThree equal weights of mass 2 kg each are hanging on a string passing over a fixed pulley as shown in fig What is the tension in the string connecting weights B and C?

View SolutionTwo blocks are connected by an inextensible light string, the string is passing over smooth, light pulley as shown. Find the acceleration of blocks and tension in the string, reaction in pulley.
View SolutionThree weights A ,B and C are connected by string as shown in the figure. The system moves over a frictionless pulley. The tension in the string connecting A and B is (where g is acceleration due to gravity)
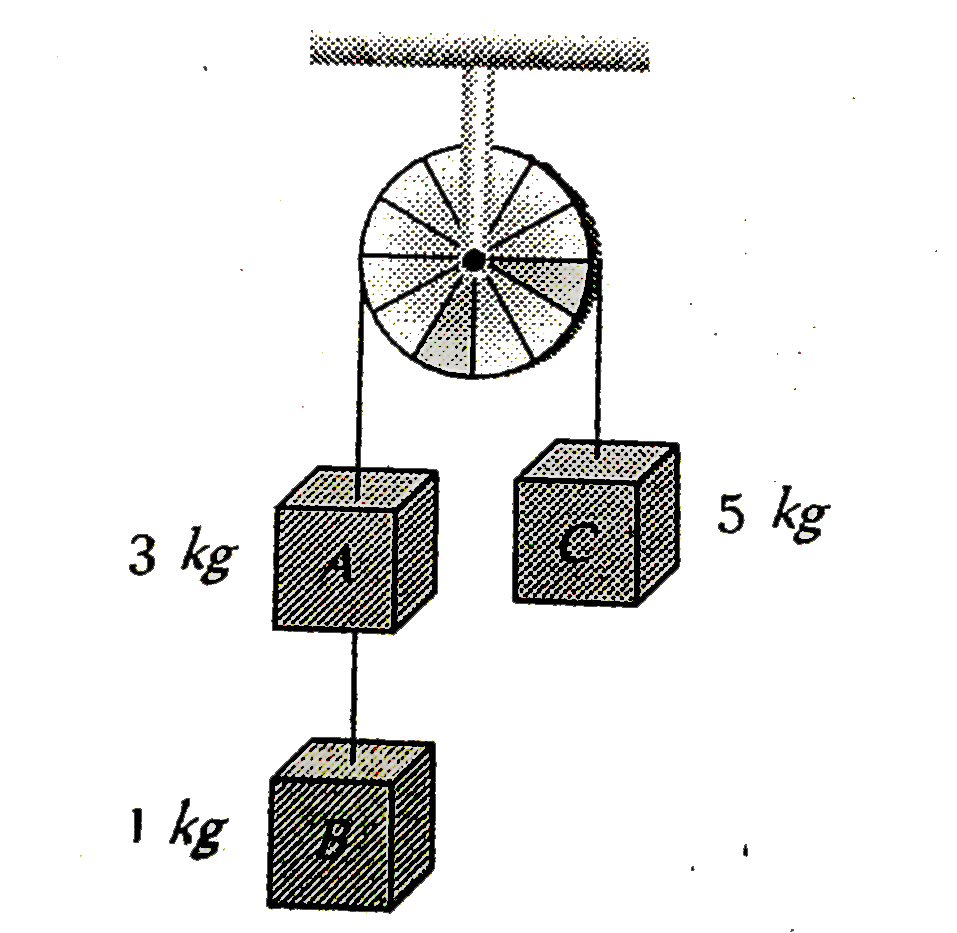
View SolutionA book of mass 5 kg is kept on a horizontal table. It is connected to a weight of mass 2 kg by a weightless string passing over a smooth pulley . The part of the string on the table is horizontal, and the weight is hanging freely from the pulley. If the coefficient of kinetic friction between the table and the block is 0.2, find the acceleration of the block. What will be the tension in the string ?
View SolutionThree equal weight and of mass each are hanging on a string passing over a fixed frictionless pulley as shown in the figure. The tension in the string connecting weights and is approximately

View SolutionThree equal weight A,B and C of mass 2kg each are hanging on a string passing over a fixed frictionless pulley as shown in the figure. The tension in the string connecting weights B and C is approximately
View SolutionThree equal weights of mass 3 kg each are hanging on a string passing over a fixed pulley as shown in figure-2.147. The tension in the string connecting weight B and C is : (Take g = 10m//s^(2) )
View SolutionTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.

View SolutionTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
View SolutionThe system shown in fig, is released from rest. Calculate the tension in the string and the force exerted by the string on the pulleys, assuming pulleys and strings are massless.

View Solution