In the network shown in Fig. using Millman’s theorem or otherwise find the voltage between A and B.
The end points of the different admittances which are connected directly to the common point B have been marked as 1 2 and 3 as shown in the Fig. Incidentally 40 Ω resistance will not be taken into consideration because it is not directly connected to the common point B. Here V01 = VA1 = −50 V ; V02 = VA2 = 100 V ; V03 = VA3 = 0 V.∴ V100 = VAb = -50/50 + 100/20 + 0/10/1/50 + 1/20 + 1/10 = 23.5VSince the answer comes out to be positive it means that point A is at a higher potential as compared to point B. The detailed reason for not taking any notice of 40 Ω resistance are given in
Related Solutions
Find the equivalent resistance of the network as shown in Fig 27.48 between points a and b
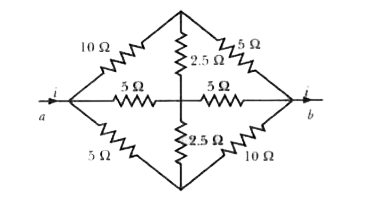
View SolutionFind the potential difference between the points A and B for the network shown in Fig. 4.52.

View SolutionFind the equivalent resistance of the networks shown in Fig. 4.51 between the points A and B.
View SolutionThe equivalent resistance between points A and B in the network shown in fig. is –
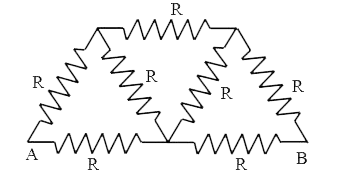
View SolutionCalculate the resistance between the terminals A and B of the network shown in fig

View SolutionIn the network shown in Fig., calculate the equivalent resistance between the points
A and B,
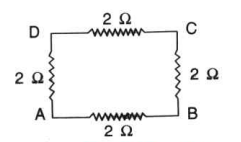
View SolutionCalculate the effective resistance between the points A and B in the network shown below in Fig.
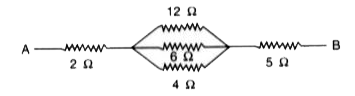
View SolutionCalculate the resistance between the terminals A and B of the network shown in fig
View SolutionConsider an infinite ladder of network shown In fig 5.223. A voltage is applied between points A and B. If the voltage is halved after each section, find the ratio of R_1//R_2 .
View SolutionCalculate the effective resistances between the points A and B in the networks shown in (Fig. 3.20) (a) and (Fig. 3.20)(b). .
View SolutionFind potential difference between points A and B of the network shown in Fig. and distribution of given main current through different resistors.
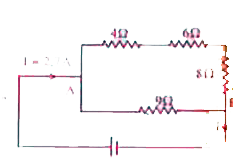
View SolutionFind potential difference between points A and B of the network shown in Fig. and distribution of given main current through different resistors.

View SolutionFind the equivalent resistance between the points A and B of the network of resistors shown in Fig. 4.16.
View SolutionFind potential difference between points A and B of the network shown in fig. and distribution of given main current through different resistors.
View SolutionIn the network shown in fig. , the potential differene across A and B is
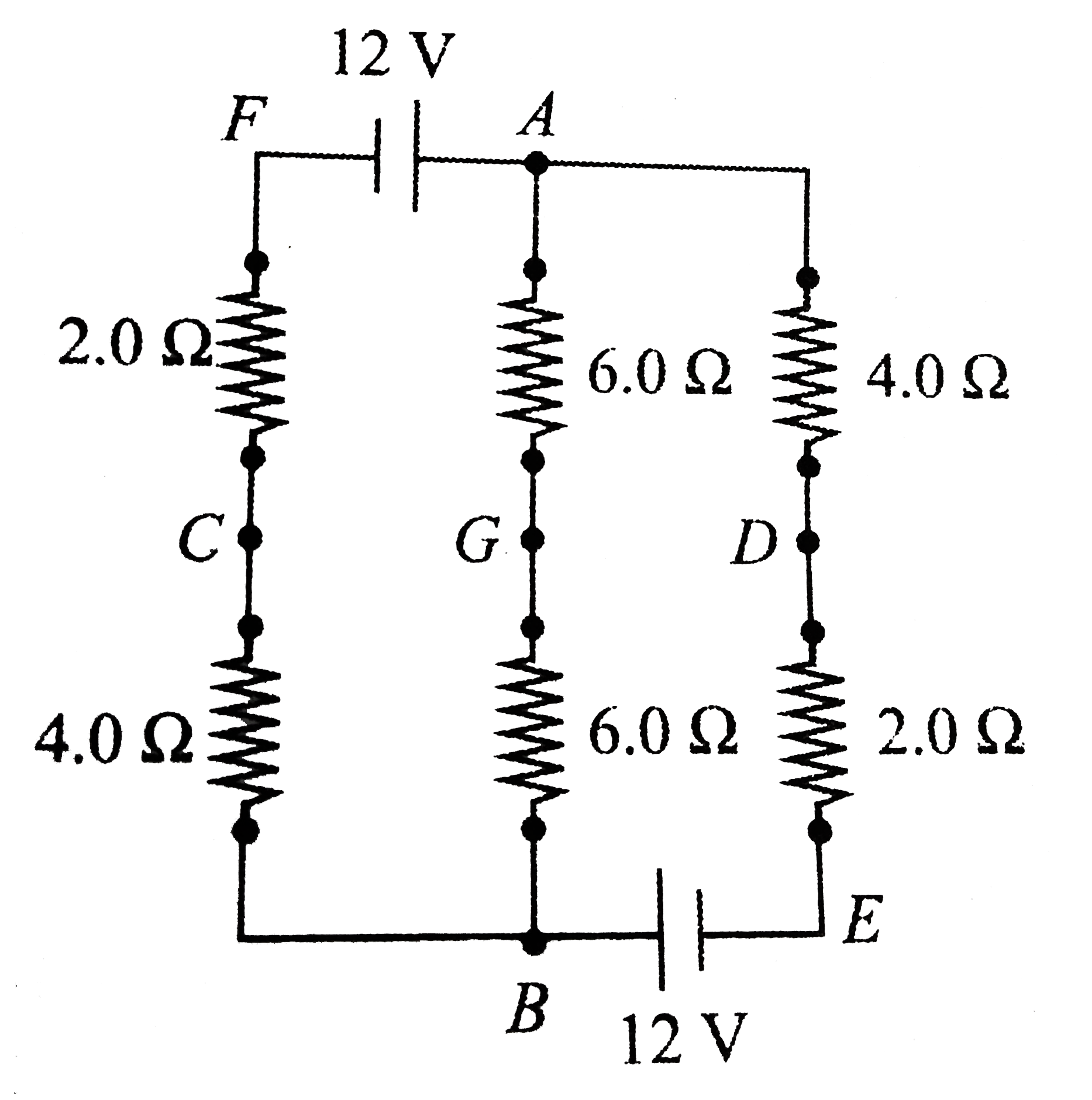
View SolutionIn the network shown in fig. , the potential differene across A and B is
View SolutionIn the network shown in Fig.

View SolutionThe equivalent resistance between A and B in the network in fig.,
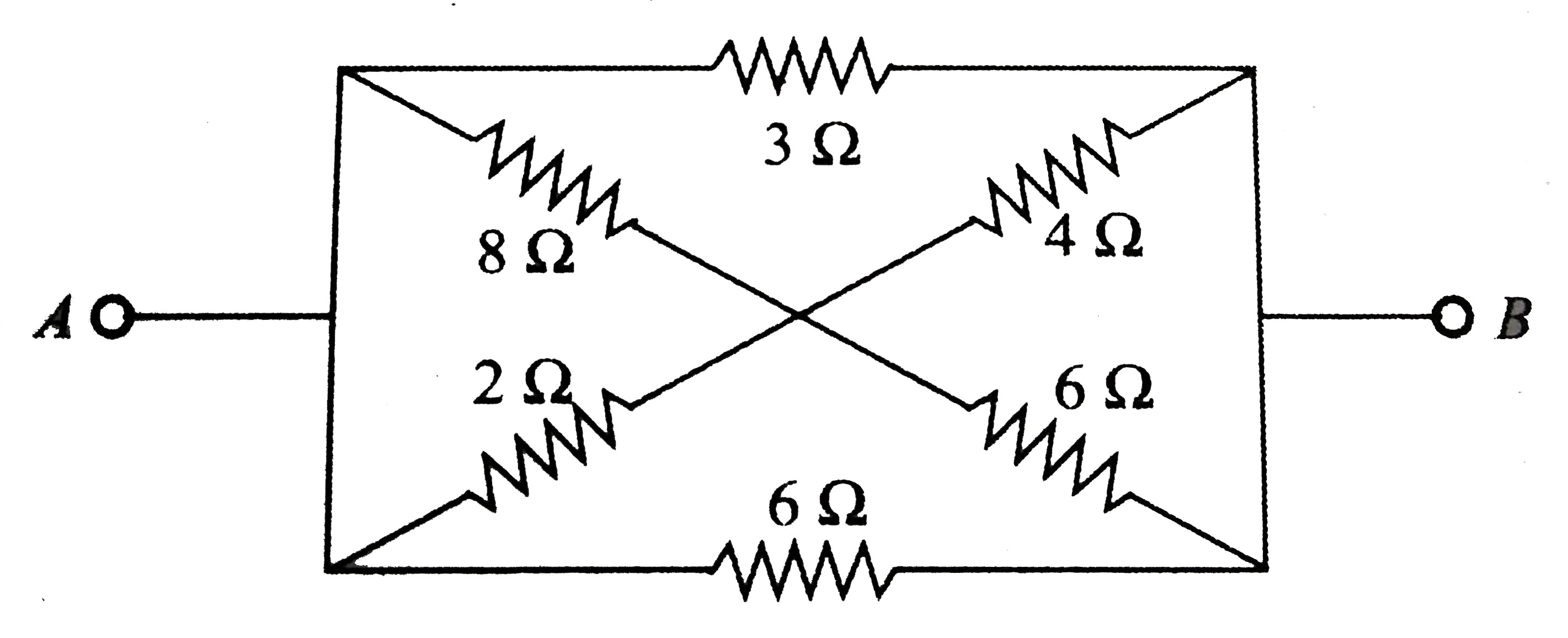
View SolutionIn the network shown in fig. each resistance is R.

The equivalent resistance between A and C is
View SolutionIn the network shown in Fig., calculate the equivalent resistance between the points A and C.
View Solution