The turning moment diagram for a multicylinder engine has been drawn to a scale 1 mm = 600 N-m vertically and 1 mm = 3° horizontally. The intercepted areas between the output torque curve and the mean resistance line taken in order from one end are as follows : + 52 – 124 + 92 – 140 + 85 – 72 and + 107 mm2 when the engine is running at a speed of 600 r.p.m. If the total fluctuation of speed is not to exceed ± 1.5% of the mean find the necessary mass of the flywheel of radius 0.5 m.
Given : N = 600 r.p.m or ω = 2 π = x 600/60 = 62.84 rad/s; R = 0.5 mSince the total fluctuation of is not to exceed ± 1.5% of the mean speed thereforeω1 - ω2 = 3% ω = 0.03ωand coefficient of fluctuation of speed Cs = ω1 - ω2/ω = 0.03The turning diagram is shownSince the turning moment scale 1 mm = 600 N-m and crank angle scale is 1 mm = 3° = 3° x π/180 = π/60rad therefore1 mm2 on turning momment diagram= 600 x π/60 = 31.42 N-mLet the total energy at A = E We known that maximum fluctuation of energy ΔE = maximum energy - minimum energy = E + 52 - E - 120 = 172 = 172 x 1.42 = 5404 N-mLet m = Mass of the flywheel in kg.We know that maximum fluctuation of energyΔE
Related Solutions
107 पेंचो के सिरों का व्यास (मिमी. में) नीचे सारणी में दिया गया है :
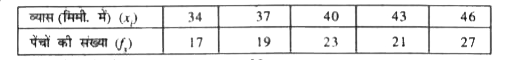
पेंचो के सिरों के व्यास का माध्य ज्ञात कीजिए ।
View SolutionThe scale on a map is 1 mm : 4 m. Find the distance on the map for an actual distance of 52 m.
View SolutionOne kg of copper is drawn into a wire of 1 mm diameter and a wire of 2 mm diameter. The resistance of the two wires will be in the ratio
View Solutionएक तार का व्यास नापने के लिए प्रयुक्त स्क्रूगेज के पाठ निम्न है : मुख्य स्केल का पाठ मिमी, वृत्तीय स्केल का पाठ खाने दिया है कि मुख्य स्केल मिमी, पर 1 वृत्तीय स्केल के 100 खानो के संगत है तार का व्यास है :
View SolutionA wire hanging vertically from one end of it is drawn by adding a load of 200 N at the lower end. If the load expands the wire by 1 mm, the elastic energy stored in the wire is -
View SolutionExpress the as indicated. One has been done for you.
20 mm as m
View SolutionEach division on the main scale is . Which of the following vernier scales give vernier constant equal to ?
View SolutionEach division on the main scale is . Which of the following vernier scales give vernier constant equal to ?
View SolutionEach division on the main scale is 1 mm . Which of the following vernier scales give vernier constant equal to 0.01 mm ?
View Solutionएक पैमाना सेन्टीमीटर से अशांकित है तथा निम्न मापन पैमाने द्वारा ज्ञात किए जाते है। सार्थक अंक ज्ञात कीजिए।
8.921 mm
View SolutionWhat is the angle between the straight lines where ?
View SolutionThe figure shown below is a screwgauge. When the circular scale division matches the main scale at 43, the 6.5 mm mark on the main scale is just visible. The main scale has (1)/(2)mm marks. In complete rotation, the screw advances by (1)/(2) mm and circular scale has 50 divisions. The reading of the screwgauge is
View SolutionThe figure shown below is a screwgauge. When the circular scale division matches the main scale at 43, the 6.5 mm mark on the main scale is just visible. The main scale has (1)/(2)mm marks. In complete rotation, the screw advances by (1)/(2) mm and circular scale has 50 divisions. The reading of the screwgauge is
View SolutionA screw gauge has 50 divisions on its circular scale and its screw moves by 1 mm on turning it by two rotations. When the flat end of the screw is in contact with the stud, the zero of circular scale lies below the base line and 4th division of circular scale is in line with the base line. Find the pitch.
View SolutionA screw gauge has 50 divisions on its circular scale and its screw moves by 1 mm on turning it by two rotations. When the flat end of the screw is in contact with the stud, the zero of circular scale lies below the base line and 4th division of circular scale is in line with the base line. Find the least count .
View SolutionOne end of a 100 cm long rod is fixed. At its free end a screw is attached and the pitch of the screw is 0.5 mm. The rod can move along its length on turning the screw. The screw has a circular scale with 100 divisions. It moves by one small scale division of 0.5 mm per turn. At 20^(@)C , the pitch scale reads a little over zero and the circular scale reads 92. When the temperature is increased to 100^(@)C , the pitch scale reading changes to a little above 4 divisions and the circular scale reading is 72. Find the coefficient of linear expansion of the material of the rod.
View Solutionthe equation x/m=kP^(1/n) According to log(x//m) And log P A diagram has been drawn between Which of the following statements regarding this diagram is not correct?
View Solutionएक खेल के मैदान में 6 मि और 11 मि लम्बे दो खम्बे लंबवत खड़े किए गए है। यदि इन खम्बो के निचले सिरों के बिच कि दुरी 12 मि हो तो उनके ऊपरी सिरों के बिच कि दुरी ज्ञात कीजिए।
View SolutionA solenoid 600 mm long has 50 turns on it and is wound on an iron rod of 7.5 mm radius. Find the flux through the solenoid when the current in it is 3 A. The relative permeability of iron is 600 :
View SolutionIf 1 litre of a gas A at 600 mm and 0.5 litre of gas B at 800 mm are taken in a 2-litre bulb, the resulting pressure is
View Solution