For the circuit shown in Fig.calculate the current in the 6 Ω resistance by using Norton’s theorem.
As explained in we will replace the 6Ω resistance by a short-circuit as shown in Fig.. Now we have to find the current passing through the short-circuited terminals A and B. For this purpose we will use the mesh analysis by assuming mesh currents I1 and I2.From mesh i we get 3 − 4 I1 − 4 I1 − I2 + 5 = 0 or 2 I1 − I2 = 2 ...i From mesh ii we get − 2 I2 − 4 − 5 − 4 I2 − I1 = 0 or 4I1 − 6I2 = 9 ...ii From i and ii above we get I2 = − 5/4 The negative sign shows that the actual direction of flow of I2 is opposite to that shown in Fig. . Hence Ish = IN = I2 = − 5/4 A i.e. current flows from point B to A. After the terminals A and B are open-circuited and the three batteries are replaced by short circuits since their internal resistances are zero the internal resistance of the circuit as viewed from these terminals’ is Ri = RN = 2 + 4 || 4 = 4 Ω The Norton’s equivalent circuit consists of a constant current source of 5/4 A in parallel with a resistance of 4 Ω as shown in Fig. . When 6 Ω resistance is connected across the equivalent circuit current through it can be found by the current-divider rule Art. Current through 6 Ω resistor = 5/4 x 4/10 = 0.5 from B to A.
Related Solutions
Three resistors of are given in the class.a) What is the highest resistance that you can get using all of them? b) What is the least resistance that you can get using all of them? c) Can you make a resistance using these three? Draw the circuit.
View SolutionIn the circuit shown in fig the voltage across the 2 Ω resistor is 12V. What is the emf of the battery and the current thorugh the 6 Ω resistor?

View SolutionIn the following circuit the equivalent resistance between A and B is
10 Ω
20 Ω
30 Ω
40 Ω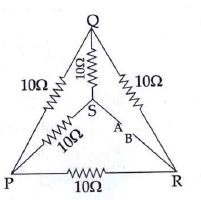
View SolutionIn the circuit shown, the current in 3Omega resistance is
View SolutionIn the circuit shown, the current in resistance is
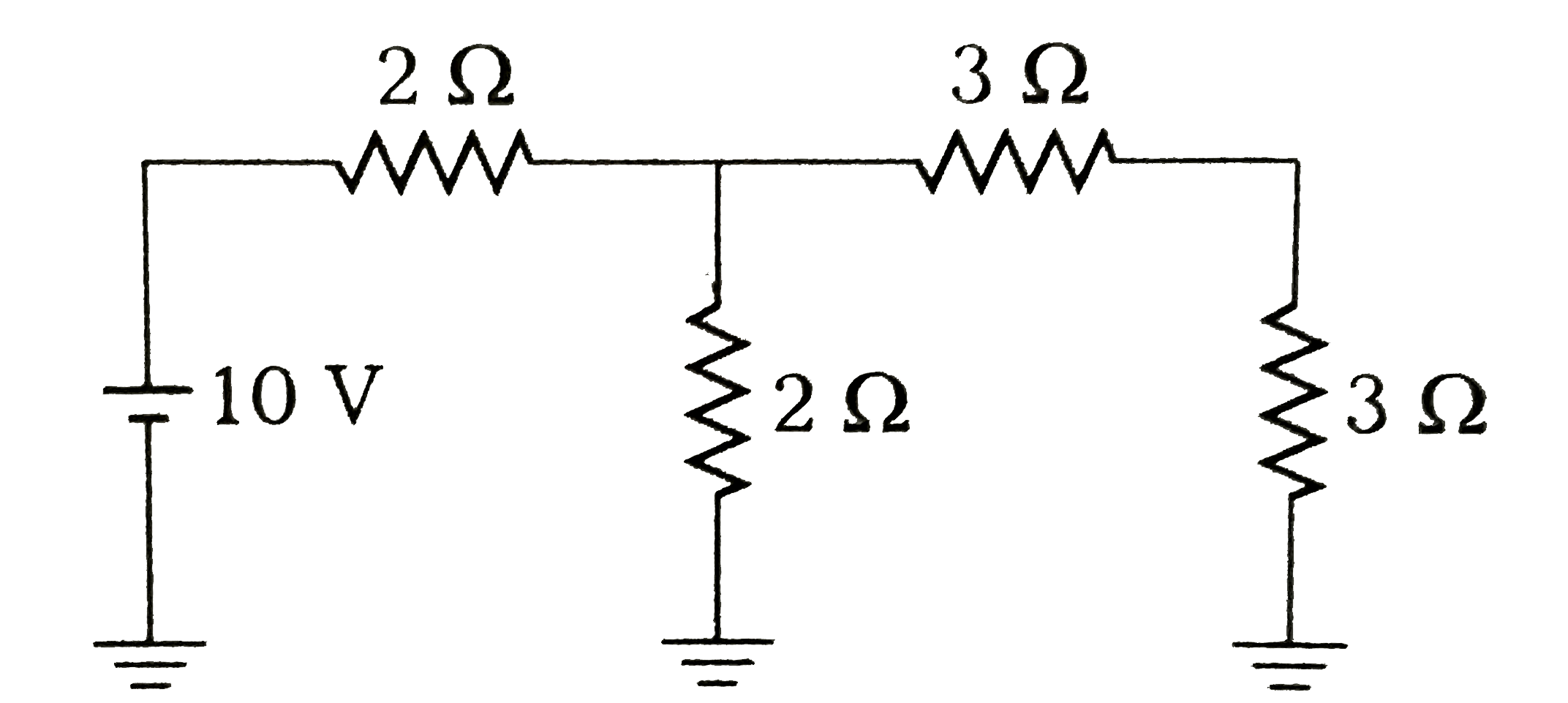
View SolutionWhen two resistors are connected to a circuit the resultant resistances are .Calculate the value of each resistor.
View SolutionChoose correct alternative. When two resistances are connected in parallel then the equivalent resistance is 6//5 Omega . When one of the resistances is removed then the effective resistance is 2 Omega . The resistance of the wire removed will be A. 3 Ω B. 2 Ω C. 3 / 5 Ω D. 6 / 5 Ω
View SolutionIn the circuit shown in the figure , no current flows through the 8 Ω resistor, then the potential difference between points A and Bis
_PHY_E01_001_Q01.png)
View SolutionFind the resistance between delta-star theorem A to B in the circuit shown in the figure.
View SolutionAmpere’s circuital theorem is generally used to determine the magnetic field produced by a current carrying element State ampere’s circuital theorem.
View Solutionचित्र में दर्शाए गए परिपथ के लिए प्रतिरोध में धारा है -
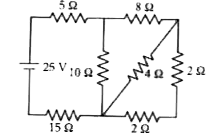
View SolutionIn the circuit shown the current through 2 resistance is
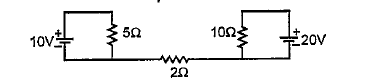
View SolutionFind the current through the resistance in the circuits shown in figure
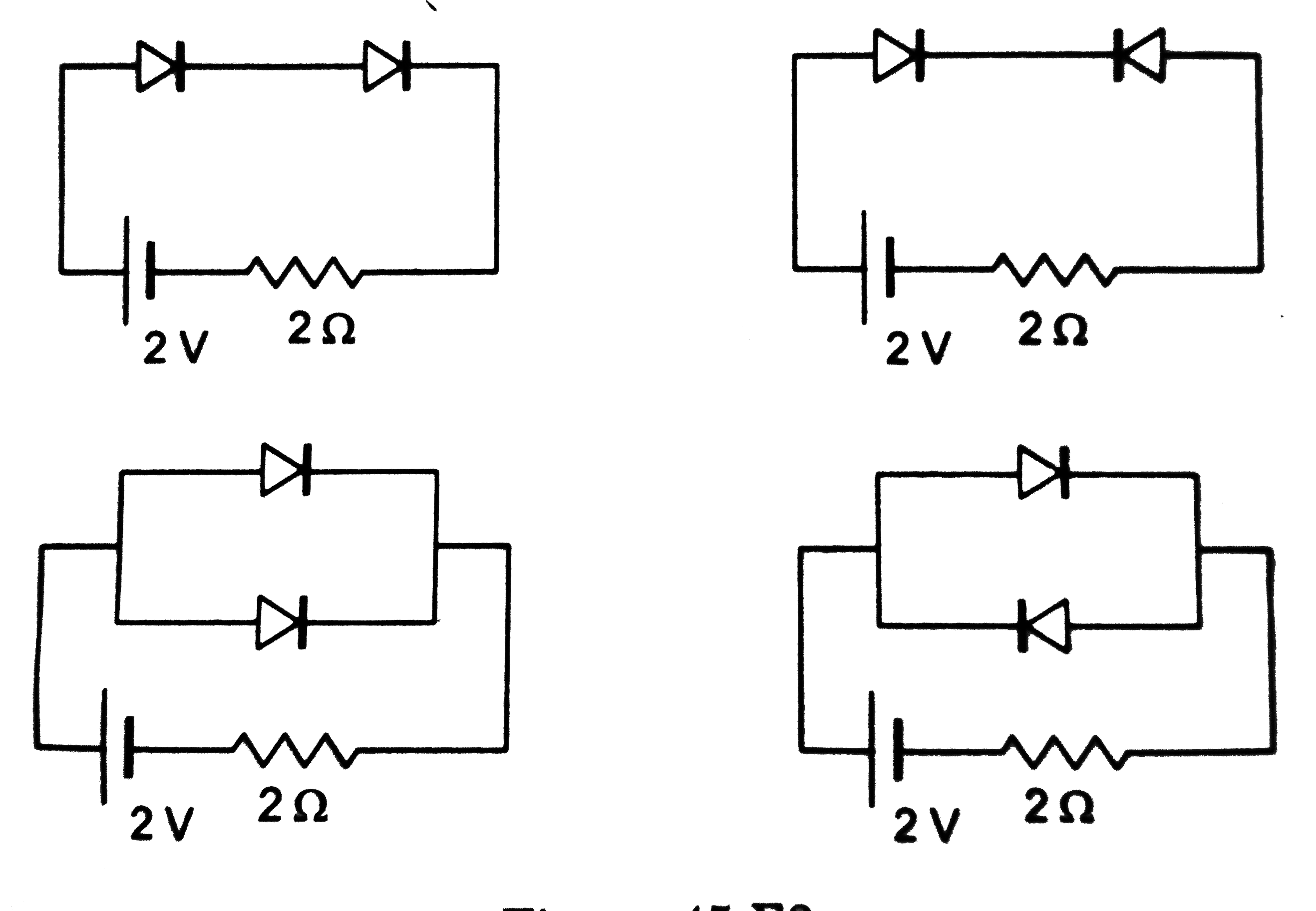
View SolutionFind the current through the resistance in the circuits shown in figure

View SolutionDetermine the currents through the resistance of the circuits shown in fig.
View SolutionIf are connected in parallel, what will be the current through the resistor?
View SolutionIn the circuit shown in the figure, find the total resistance of the circuit and current in CD arm.
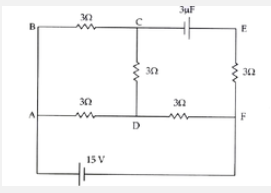
View SolutionIn the circuit shown below, calculate the total resistance of the circuit and the current flowing through it.
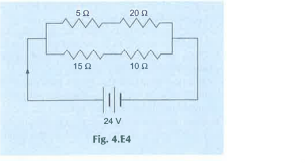
View SolutionIn the electric ntework shown in the figure, use Kirchhoffs rules to calculate the power consumed by the resistance
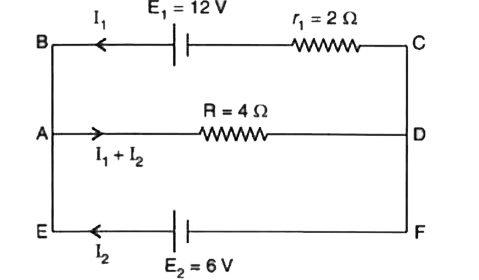
View SolutionFind the equivalent resistance and current in 6Omega resistance in the circuit shown in figure 3.55.
View Solution