Show that the straight lines ax2 + 2hxy + by2 = 0 and the straight lines ax2 + 2hxy + by2 + 2gx + fy + c = 0 form a rhombus if a - bfg + hf2 - g2 = 0.
The given pairs of lines form a parallelogram. Also the diagonals of the parallelogram are2gx + 2fy + c = 0 and yhf - bg = x gh - afThe parallelogram is a rhombus if the diagonals are at right angles see Fig. That is if the product of their slopes is equal to -1 :
Related Solutions
If the equation
represents two straights lines, then the product of the perpendicular from the origin on these straight lines, is
View SolutionIf the equation
represents two straights lines, then the product of the perpendicular from the origin on these straight lines, is
View SolutionIf the equation
represents two straights lines, then the product of the perpendicular from the origin on these straight lines, is
View SolutionIf the equation represents two straight lines, then show that they form a rectangle of area with the coordinate axes.
View SolutionIf the equation represents two straight lines, then show that they form a rectangle of area with the coordinate axes.
View SolutionIf the equation 2hxy + 2gx + 2fy + c = 0 represents two straight lines, show that they form a rectangle of area with the co-ordinate axes.
View SolutionIf the equation represents two straight lines, then show that they form a rectangle of area with the coordinate axes.
View SolutionIf the equation represents two straight lines, then show that they form a rectangle of area with the coordinate axes.
View SolutionIf represents parallel straight lines, then
View SolutionIf the straight lines ax^(2)+2hxy+by^(2)+2gx+2fy+c=0 intersect on the X -axis,then
View SolutionIf represents parallel straight lines, then
View SolutionIf represents two parallel straight lines, then
View SolutionIf represents two parallel straight lines, then
View Solutionrepresents two parallel straight lines if
View SolutionIf the pair of lines form a rhombus then prove that .
View SolutionIf the lines ax2+2xy+by2=0 meet the line px+qy=pq in points which are equidistant fromthe origin,prove that h(p?-q?)=pq(a- b)
View SolutionIf
represents a pair of straight lines , prove that the equation of the third pair of straight lines passing through the points where these meet the axes is ax^2 −2hxy+by 2 +2gx+2fy+c+ c 4fg xy=0.
View SolutionIf
represents a pair of straight lines , prove that the equation of the third pair of straight lines passing through the points where these meet the axes is =0.
View SolutionLet y = mx and be the lines represented by the equation ax2+2hxy+by+=0. Match the following and choose the correct answer.
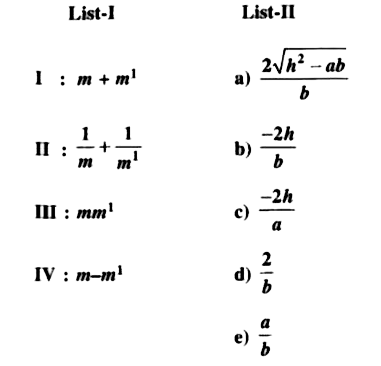
View SolutionIf the equation ax^(2)+2hxy+by^(2)+25x+2fy+c=0 represents a pair of straight lines,prove that the third pair of straight lines (excluding xy=0) passing through the points where these meet the axes is ax^(2)2hxy+by^(2)+2gx+2fy+c+(4fg)/(c)*xy=0
View Solution