For complex numbers z and ω prove that |z|2ω – |ω|2 z = z – ω if and only if z = ω or zω = 1.
|Z|2w – |w2 |Z = Z – w|Z|2 w – Z = Z – ww – Z |Z|2 + 1 = 0 ⇒ w = x
Related Solutions
The value of (1−ω+ω^2 )^ 5 +(1+ω−ω^ 2 )^ 5 where ω and ω^ 2 are the complex cube roots of unity, is
View Solutioni) (1 + ω) (1 + ω ^ 4) (1 + ω ^ 8) = -ω ^ 2
View SolutionIf are connected in parallel, what will be the current through the resistor?
View SolutionIn the following circuit the equivalent resistance between A and B is
10 Ω
20 Ω
30 Ω
40 Ω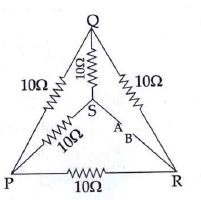
View Solutionइकाई के घन मूल #!# &
View SolutionWhat is the effective resistance (in Ω) of two resistors 21 Ω and 28 Ω connected in parallel?
View SolutionWhen two resistors are connected to a circuit the resultant resistances are .Calculate the value of each resistor.
View SolutionAn alternating current is given by 1 = 1 1 cos ω t + 1 2 sin ω t . sinomega t .The value of rms current is
View SolutionChoose correct alternative. When two resistances are connected in parallel then the equivalent resistance is 6//5 Omega . When one of the resistances is removed then the effective resistance is 2 Omega . The resistance of the wire removed will be A. 3 Ω B. 2 Ω C. 3 / 5 Ω D. 6 / 5 Ω
View SolutionA girl has many resistors of 2 Ω 9 Ω resistance. For this draw a cicuit with the minimum number of resistors.
View SolutionThree resistors of are given in the class.a) What is the highest resistance that you can get using all of them? b) What is the least resistance that you can get using all of them? c) Can you make a resistance using these three? Draw the circuit.
View SolutionFor complex numbers z and w, prove that if and only if z=w or .
View Solutionसम्मिश्र संख्याओं तथा के लिए सिद्ध कीजिए कि होगा यदि या हो।
View SolutionChoose correct alternative. A thick wire of resistance 25 Omega is drawn into a thin wire such that itslength becomes four times. The new resistance of the wire will be A. 50 Ω B. 25 Ω C. 100 Ω D. 400 Ω
View SolutionFor complex numbers , prove that , if and only if or .
View SolutionFor complex numbers , prove that , if and only if or .
View SolutionFor complex numbers z and w, prove that |z|^(2)w-|w|^(2)z=z-w, if and only if z=w or zbar(w)=1.
View SolutionIn the circuit shown in fig the voltage across the 2 Ω resistor is 12V. What is the emf of the battery and the current thorugh the 6 Ω resistor?

View Solutionमाना z एक सम्मिश्र संख्या इस प्रकार है कि तथा , तो सिद्ध कीजिये | z | =1.
View Solutionयदि , जहाँ z एक सम्मिश्र संख्या है तो सिद्ध कीजिये कि
View Solution