Using Node voltage method find the current in the 3Ω resistance for the network shown in Fig.
As shown in the figure node 2 has been taken as the reference node. We will now find the value of node voltage V1. Using the technique developed in we getV11/5 + 1/2 + 1/2 - 4/2 - 4 + 2/5 = 0The reason for adding the two battery voltages of 2 V and 4 V is because they are connected in additive series. Simplifying above we get V1 = 8/3 V. The current flowing through the 3 Ω resistance towards node 1 is = 6 - 8/3/3 + 2 = 2/3AAlternatively6 - V1/5 + 4/2 - V1/2 = 012 - 2V1 + 20 - 5V1 = 07V1 = 32Also 6 - V1/5 + 4 - V1/2 = V1/212 - 2V1 + 20 - 5V1 = 5V112V1 = 32; V1 = 8/3
Related Solutions
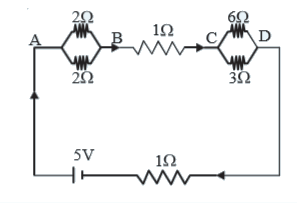
A network of resistances is connected to a 16V battery with internal resistance of 1W as shown in Fig. Obtain the voltage drops VAB, VBC and VCD.
View SolutionFind the equivalent resistance of the network as shown in Fig 27.48 between points a and b
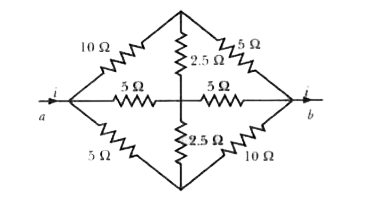
View SolutionFind the equivalent resistance of the networks shown in Fig. 4.51 between the points A and B.
View SolutionA network of resistors is connected to a 5 V battery with internal resistance of as shown in Fig. (a) Compute the equivalent resistance of the network. (6) Obtain the current in each resistor. (c) Obtain the voltage drops and
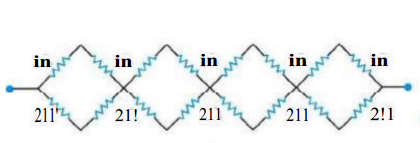
View SolutionDetermine the equivalent resistance of networks shown in Fig. 3.31. :
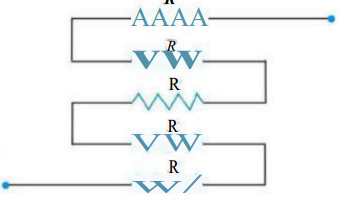
View SolutionDetermine the equivalent resistance of networks shown in Fig.

View Solutionचित्र में प्रदर्शित नेटवर्क का प्रभापि प्रतिरोध ज्ञात कीजिए तथा बैटरी से ली जाने वाली धारा| ज्ञात कीजिए|
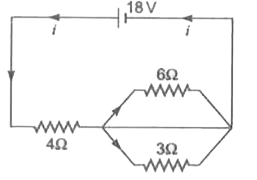
View SolutionDetermine the current in each branch of the network shown in Fig.
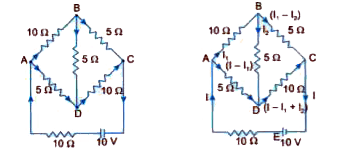
View SolutionDetermine the current in each branch of the network shown in fig.
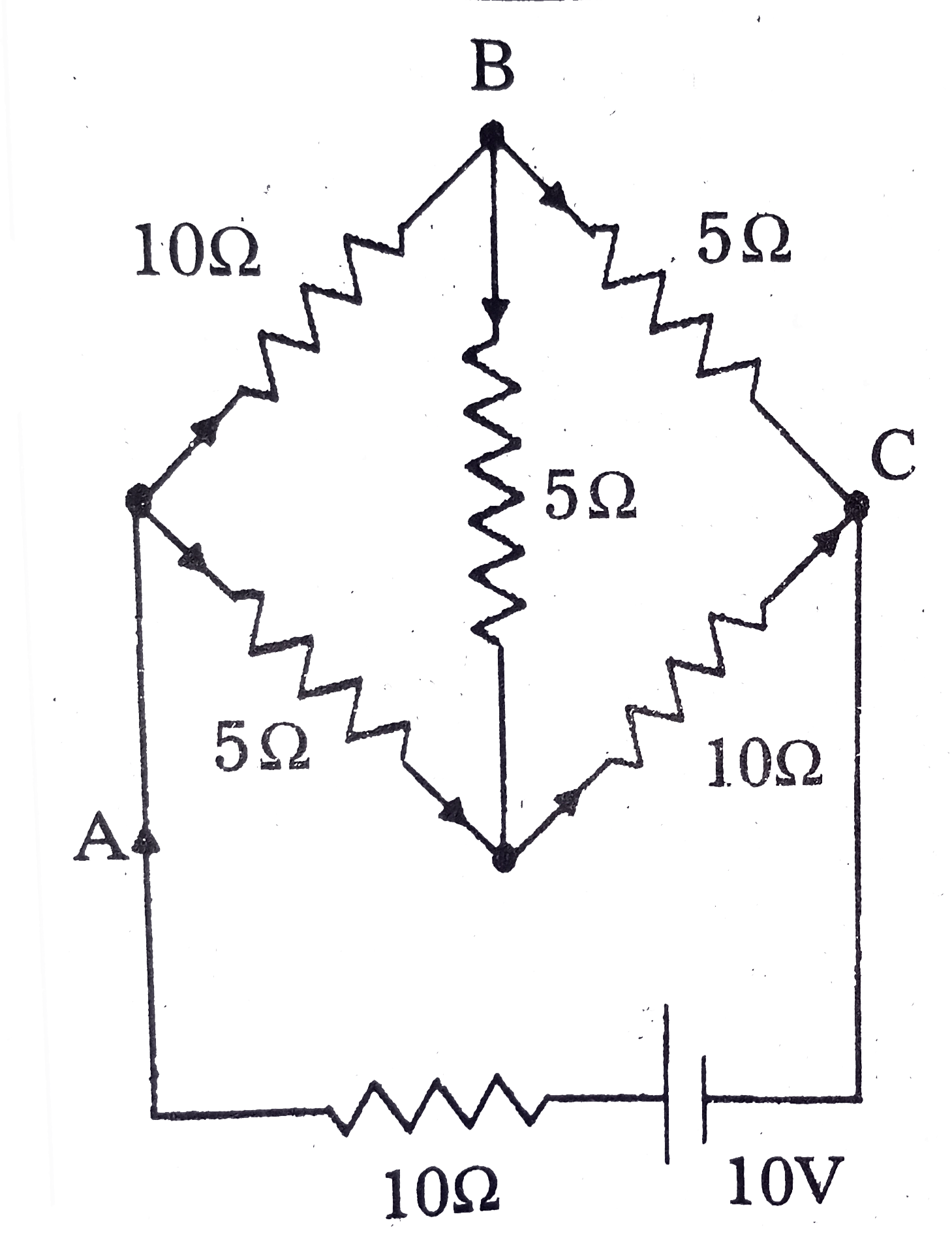
View SolutionDetermine the current in each branch of the network shown in Fig.
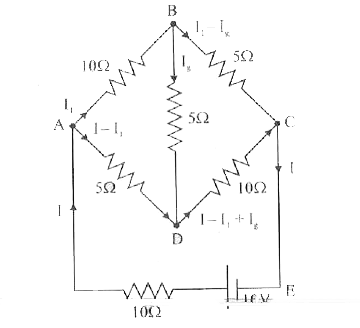
View SolutionDetermine the current in each branch of the network shown in fig.
View SolutionDetermine the current in each branch of the network shown in fig.
View Solution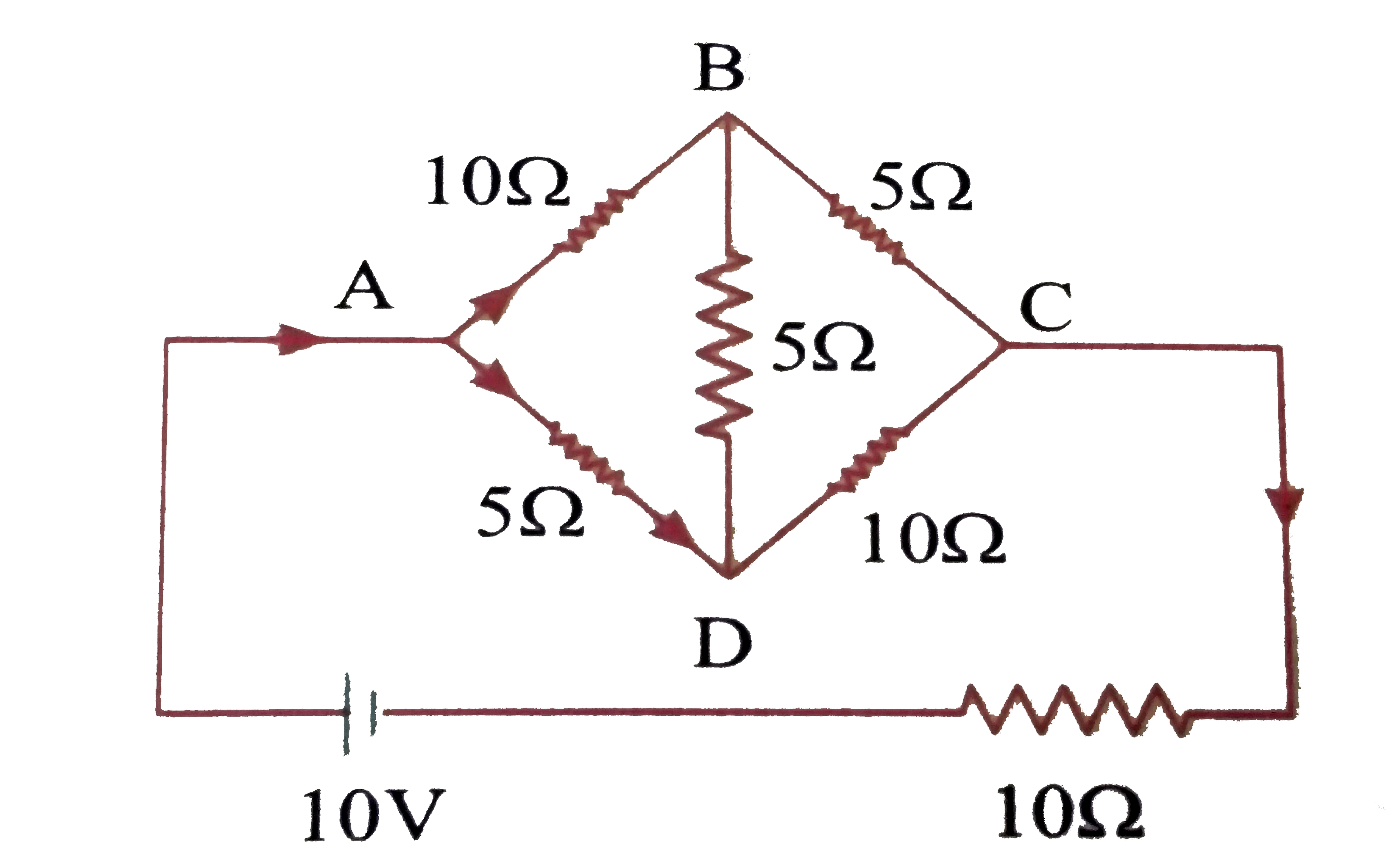
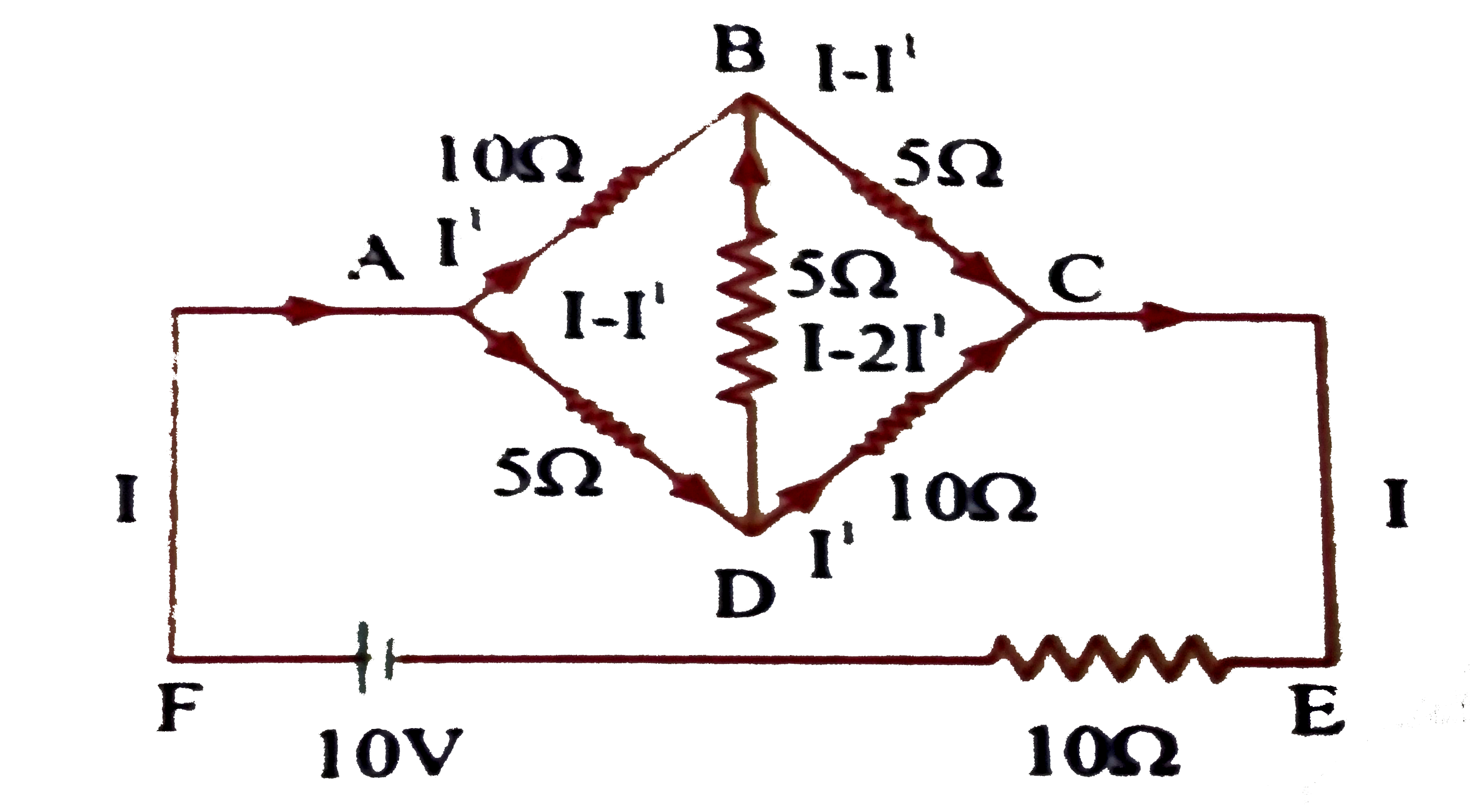
Determine the current in each branch of the network shown in fig.
View SolutionDetermine the current in each branch of the network shown in Fig.
View SolutionIn the network shown in fig. each resistance is R.

The equivalent resistance between A and C is
View SolutionA network of resistances is connected to a 16V battery with internal resistance of 1 Omega as shown in Fig. Compute the equivalent resistance of the network
View SolutionFind the current l through then resistance in the network shown in figure.
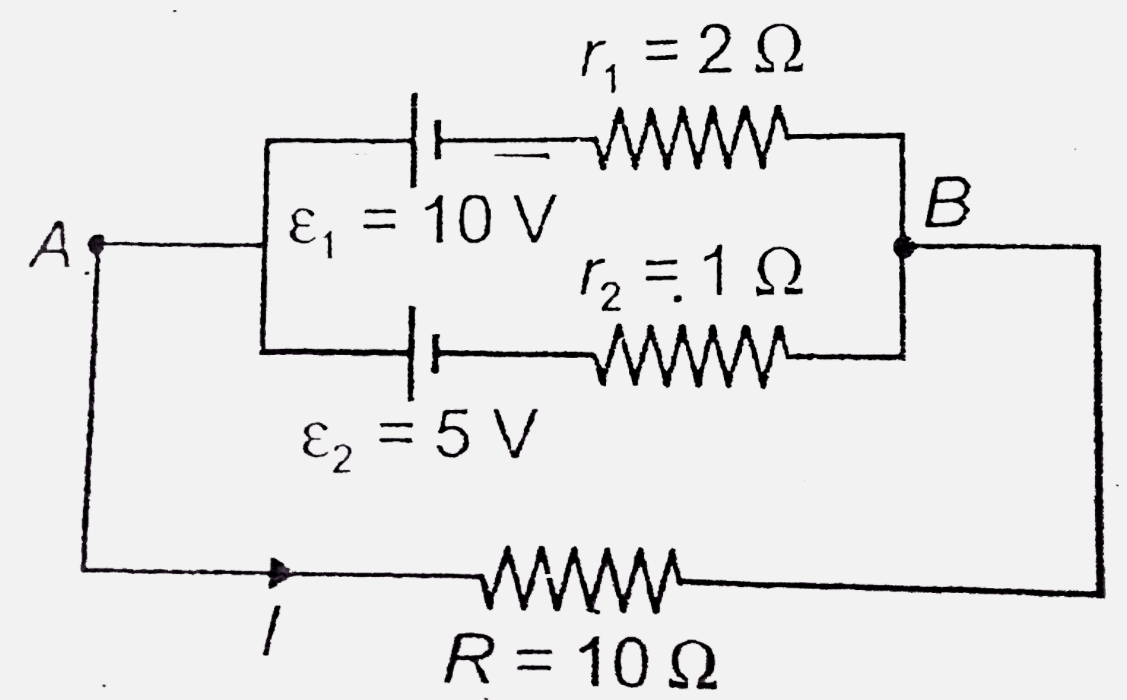
View SolutionFind the current l through then 10 Omega resistance in the network shown in figure.
View Solution10 in the network shown in the figure Omega Find the I current across the resistance.
View Solution