A block weighing 200N is in contact with an inclined plane Inclination = 30º. Will the block move under its own weight. Determine the minimum force applied 1 parallel 2 perpendicular to the plane to prevent the motion down the plane. What force P will be required to just cause the motion up the plane µ = 0.25?
Consider the FBD of block as shown in figaFrom the equilibrium condition Sum of forces perpendicular to plane = 0 R – W cos 30° = 0; R = W cos 30° ...i Sum of forces parallel to plane = 0 µR – W sin 30° = 0Now body will move down only if the value of µR is less than Wsin30° Now µR = 0.25 × W0.866 = 0.2165W ...iii And Wsin30° = 0.5W ...vi Since value of iv is less than value of iii So the body will move down. i When Force acting parallel to plane as shown in fig b Frictional force is acting up the plane∑V = 0; R = 0.216 W ...v ∑H = 0; P = W sin 30° – µR P = 0.5 × 200 – 0.216 × 200P = 56.7Nii When Force acting perpendicular to plane as shown in figc Frictional force is acting up the plane ∑H = 0; Wsin30° – µR = 0 R = 400 ...vii ∑V = 0; P + R = W cos 30° P = 0.866 × 200 – 400 P = –226.79Niii The force P required to just cause the motion up the plane as shown in figd Frictional force is acting down the plane Sum of force perpendicular to plane = 0 R = W cos 30 = 172.2N ...viii Sum of force Parallel to plane = 0 P – µR – W sin 30 = 0 P = 0.25 × 172.2 – 200 sin 30 P = 143.3N
Related Solutions
A block of mass is placed on a rough inclined plane. When the inclination of the plane is , the block just beging to slide down the plane under its own weight. The minimum force applied parallel to the plane, to move the block up the plane, is.
View SolutionA block of mas M is resting on an inclined plane as shown in the figure. The inclination of the plane to the horizontal is gradually increased. It is found that when the angle of inclination is the block just begins to slide down the plane. What is the minimum force F applied parallel to the plane that would just make the block move up the plane ?
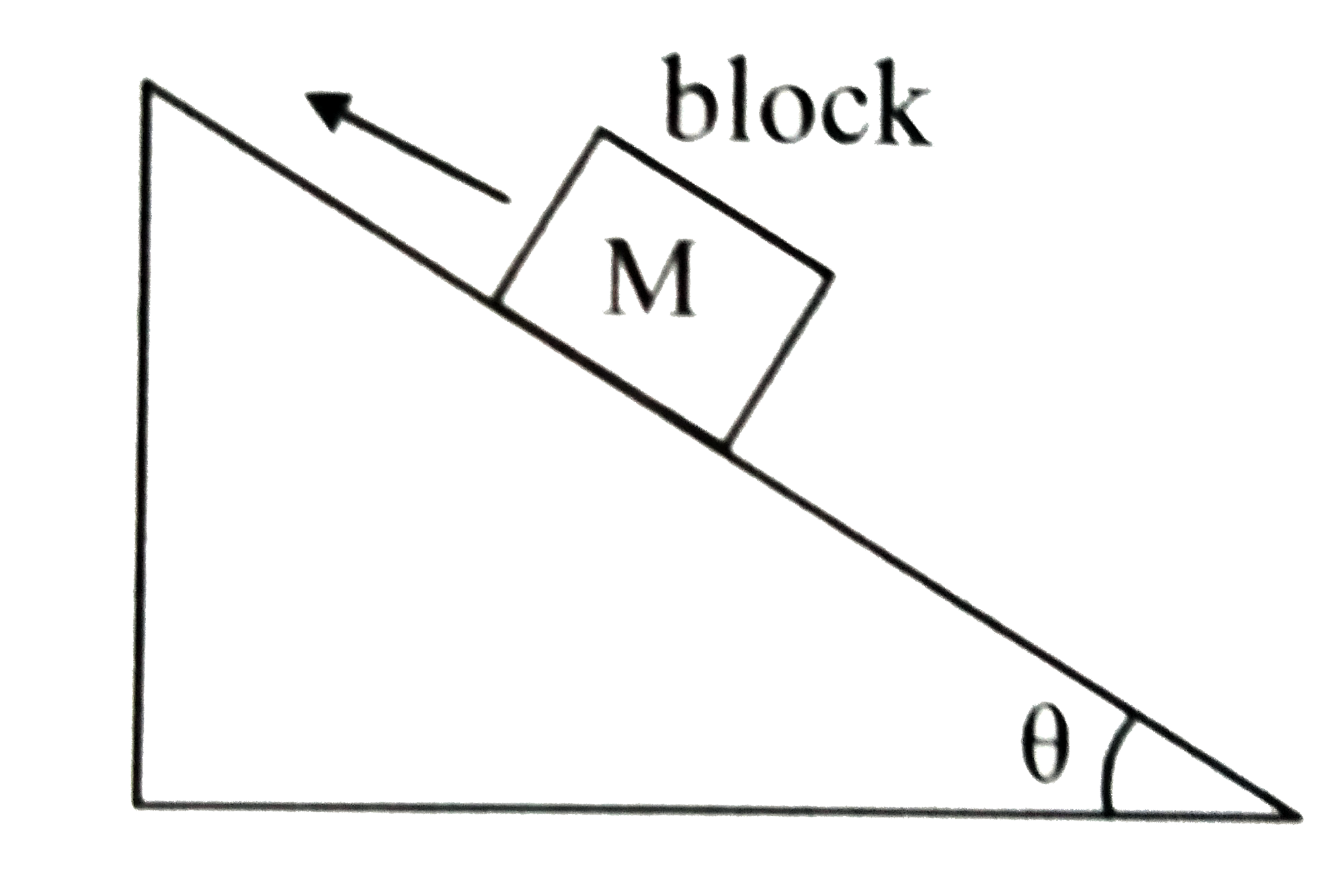
View SolutionA block of mass m is resting on an inclined plane. The inclination of the plane to the horizontal is gradually increased. It is found that when angle of inclination is theta , the block just begins to slide down the plane. What is the minimum force F applied parallel to the plane that would just make the block move up the plane?
View SolutionA block of mas M is resting on an inclined plane as shown in the figure. The inclination of the plane to the horizontal is gradually increased. It is found that when the angle of inclination is the block just begins to slide down the plane. What is the minimum force F applied parallel to the plane that would just make the block move up the plane ?

View SolutionA block of mas M is resting on an inclined plane as shown in the figure. The inclination of the plane to the horizontal is gradually increased. It is found that when the angle of inclination is the block just begins to slide down the plane. What is the minimum force F applied parallel to the plane that would just make the block move up the plane ?

View SolutionA block of weight 1 N rests on a inclined plane of inclination with the horizontal. The coefficient of friction between the block and the inclined plane is . The minimum force that has to be applied parallel to the inclined plane to make the body just move up the plane is
View SolutionA block of weight 1 N rests on a inclined plane of inclination theta with the horizontal. The coefficient of friction between the block and the inclined plane is mu . The minimum force that has to be applied parallel to the inclined plane to make the body just move up the plane is
View SolutionThe force required just to move a body up an inclined plane is double the force required just to prevent the body sliding down. If the coefficient of friction is 0.25, what is the angle of inclination of the plane ?
View SolutionThe force F_(1) required to just moving a body up an inclined plane is double the force F_(2) required to just prevent the body from sliding down the plane. The coefficient of friction is mu . The inclination theta of the plane is :
View SolutionThe force F_(1) required to just moving a body up an inclined plane is double the force F_(2) required to just prevent the body from sliding down the plane. The coefficient of friction is mu . The inclination theta of the plane is :
View SolutionA block of weight w rests on a horizontal plane. A force P inclined at an angle theta to the plane is applied to the block until it is on the of motion. Find the value of coefficient of friction.
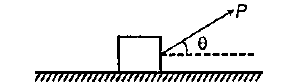
View SolutionThe force required just to move a body up an inclined plane is double the force required just to prevent the body sliding down. If the coefficient of friction is 0.25 , the angle of inclination of the plane is
View SolutionThe minimum force required to move a body upwards on an inclined plane is three times the minimum force required to prevent it from sliding down the plane. If the coefficient of friction between the body and the inclined plane is, then the angle of the inclined plane is:
View SolutionAn inclined plane is inclined at an angle when the block placed on it is just at the point of moving down the plane. What can be minimum acceleration with which the block can be moved up the inclined plane?
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination . If coefficient of friction between the block and the inclined plane is , then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination theta . If coefficient of friction between the block and the inclined plane is mu , then the minimum value of force along the plane required to move the block on the plane is
View SolutionThe minimum force required to move a body up an inclined plane of inclination 30° is found to be thrice the minimum force required to prevent if from sliding down the plane. The co-efficient of friction between the body and the plane is -
View SolutionA block of mass 2kg is lying on a rough inclined plane. The force needed to move the block up the plane with uniform velocity by applying a force parallel to the plane is 100N. The force needed to move the block up with an accele-ration of is
View SolutionMinimum Force Required to Move a body|Motion on Rough Incline Plane
View SolutionMinimum Force Required To Move The Particle|Motion On A Rough Inclined Plane
View Solution