Show that the product of the perpendicular distances of the lines ax2 + 2hxy + by2 = 0 from a point x0 y0 is
Suppose the given lines are l1x + m1y = 0 and l2x + m2y = 0 so thatl1l2 = al1m2 + l2m2 = 2hand m1m2 = bSee Fig. Let d1 and d2 be the distances of the lines from Px0 y0. Therefore we haveHence
Related Solutions
A straight line which make equal intercepts on +ve x and y axes and which is at a distance '1' unit from the origin intersects the straight line y=2x+3+sqrt2 at (x0,y0) then 2x0+y0 =
View SolutionFind the product of the perpendiculars drawn from the point on the lines
View SolutionFind the product of the perpendiculars drawn from the point on the lines
View SolutionFind the product of the perpendiculars drawn from the point on the lines
View SolutionFind the product of the perpendiculars drawn from the point on the lines
View SolutionFind the product of the perpendiculars drawn from the point on the lines
View SolutionThe product of the perpendicular drawn from the point on the lines represented by is ………
View SolutionIf the product of the perpendiculars drawn from the point (1,1) on the lines is 1, then
View SolutionIf the product of the perpendiculars drawn from the point (1,1) on the lines is 1, then
View SolutionShow that the product of the perpendicular from (alpha,beta) to the pair of lines is Hence or otherwise find the product of the perpendicular from the origin
View SolutionIf the lines ax2+2xy+by2=0 meet the line px+qy=pq in points which are equidistant fromthe origin,prove that h(p?-q?)=pq(a- b)
View SolutionFind the equations of the tangent and normal to the hyperbola at the point
View SolutionProduct of the perpendiculars from to the lines is
View SolutionShow that product of the perpendicular distances from origin to pair of lines represented by is
View SolutionShow that product of the perpendicular distances from origin to pair of lines represented by is
View SolutionThe product of the perpendicular distances from the point (-2,3) to the lines is
View SolutionIf the equation
represents two straights lines, then the product of the perpendicular from the origin on these straight lines, is
View SolutionIf the equation
represents two straights lines, then the product of the perpendicular from the origin on these straight lines, is
View SolutionIf the equation
represents two straights lines, then the product of the perpendicular from the origin on these straight lines, is
View SolutionLet y = mx and be the lines represented by the equation ax2+2hxy+by+=0. Match the following and choose the correct answer.
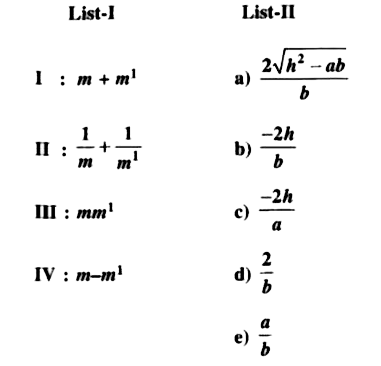
View Solution