Determine the voltages 1 and 2 of the network in Fig. by nodal analysis.
Write the conductance matrix for the network with nodes numbered as 1 2 4 as shown.g11 = 1 + 0.5 + 0.5 = 2 mho g22 = 1 + 0.5 = 1.5 mho g33 = 1 mho g12 = 0.5 mho g23 = 0 g13 = 1mhoThis gives V1 = Δ1/Δ = 2.50/1.25 = 2 Volts And V2 = Δ2/Δ = 2.50/1.25 = 2 Volts It means that the 2-ohm resistor between nodes 1 and 2 does not carry current.
Related Solutions
Nodal Analysis #!#Part 1
View SolutionNODAL ANALYSIS #!#Part 3#!#Solving circuits using Nodal analysis
View SolutionNodal Analysis #!#Part 2#!#KCL
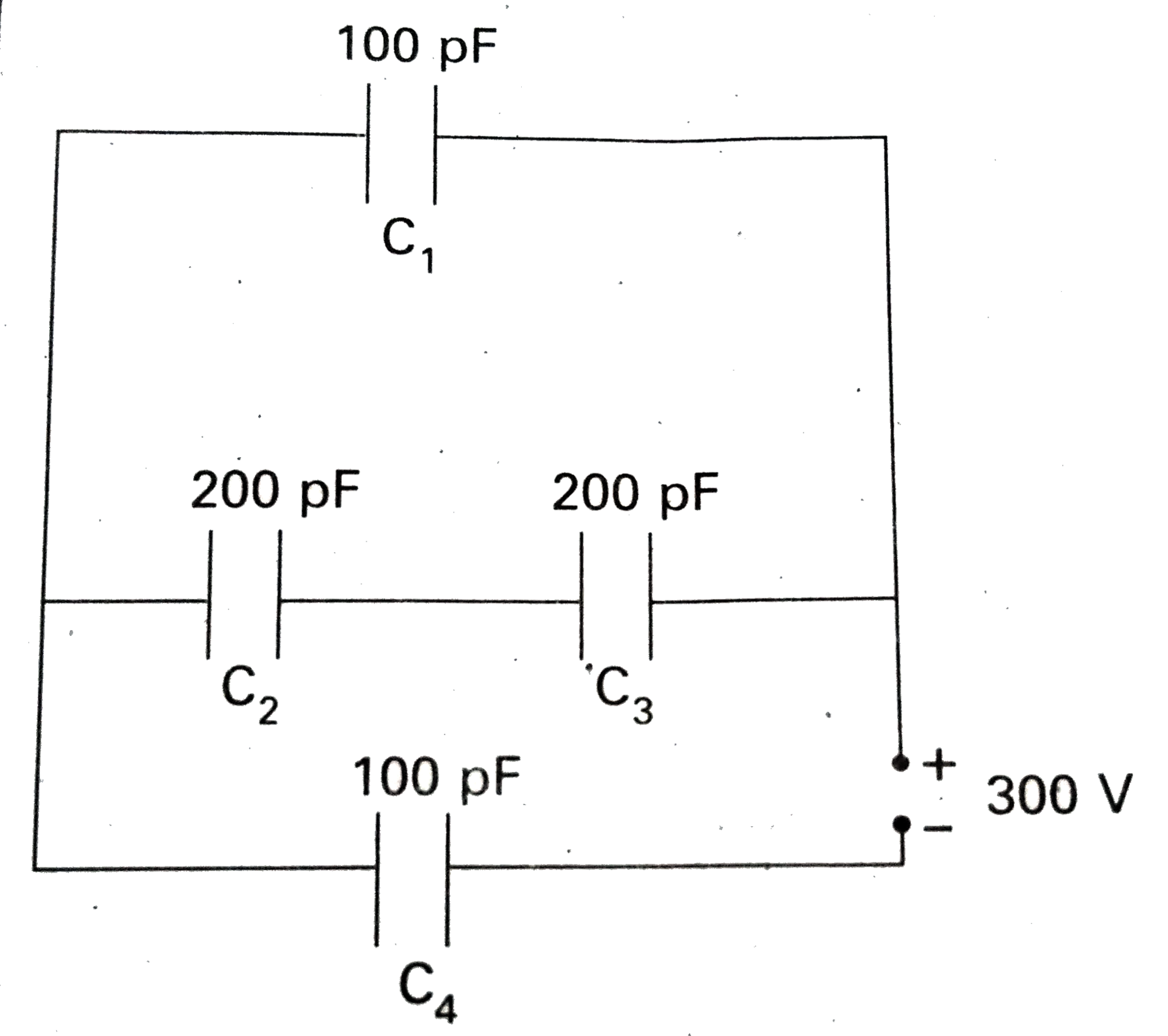
View SolutionObtain the equivalent capacitance of the network in Fig. For a 300 V supply, determine the charge and voltage across each 100 pF capacitor.
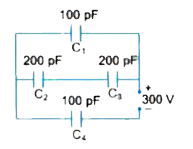
View SolutionObtain the equivalent capacitance of the following network in Fig. For 300 V supply, determine the charge and voltage across each capacitor. :
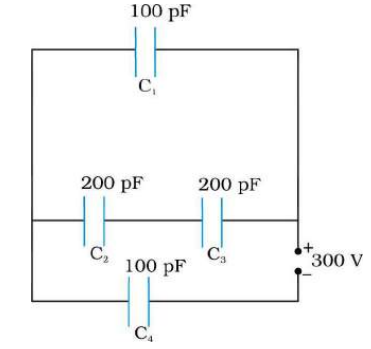
View SolutionObtain equivalent capacitance of the following network, Fig. For a 300V supply determine the charge and voltage across each capacitor.
View SolutionObtain the equivalent capacitance of the network in Fig. 2.33. For a 300 V supply, determine the charge and voltage across each capacitor.
View SolutionObtain the equivalent capacitance of the network in Fig. For a 300 V supply. Determin the change and voltage across each capacitor.
View SolutionNodal Method Of Circuit Analysis
View SolutionNodal Analysis, Combination of Cells
View SolutionDetermine the equivalent resistance of networks shown in Fig. 3.31. :
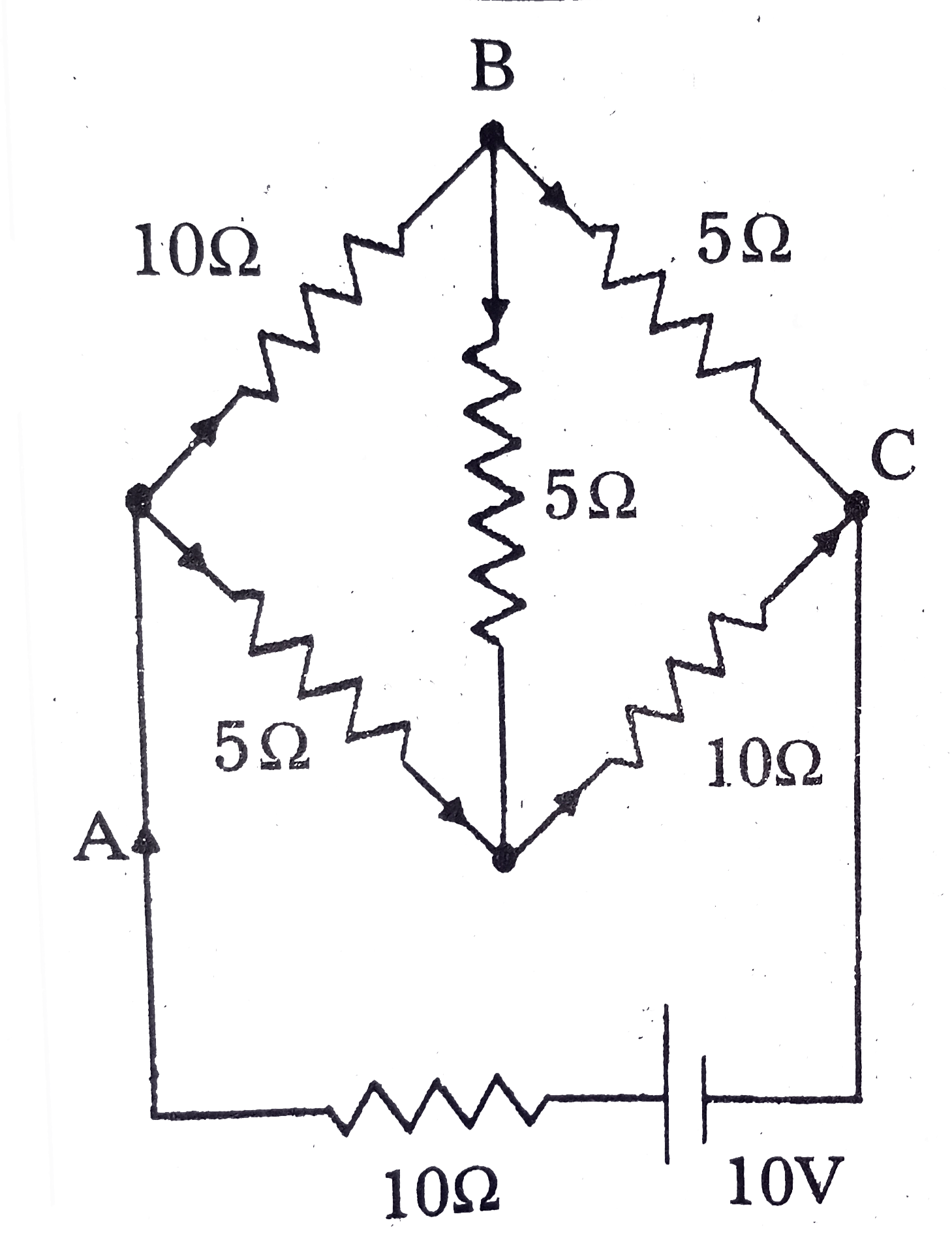
View SolutionDetermine the current in each branch of the network shown in Fig.
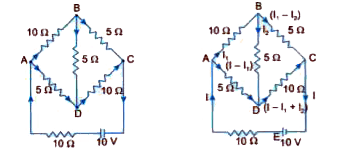
View SolutionDetermine the current in each branch of the network shown in fig.
View SolutionDetermine the equivalent resistance of networks shown in Fig.

View SolutionDetermine the current in each branch of the network shown in Fig.
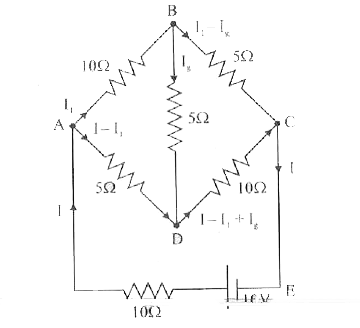
View SolutionDetermine the current in each branch of the network shown in fig.
View SolutionDetermine the current in each branch of the network shown in fig.
View Solution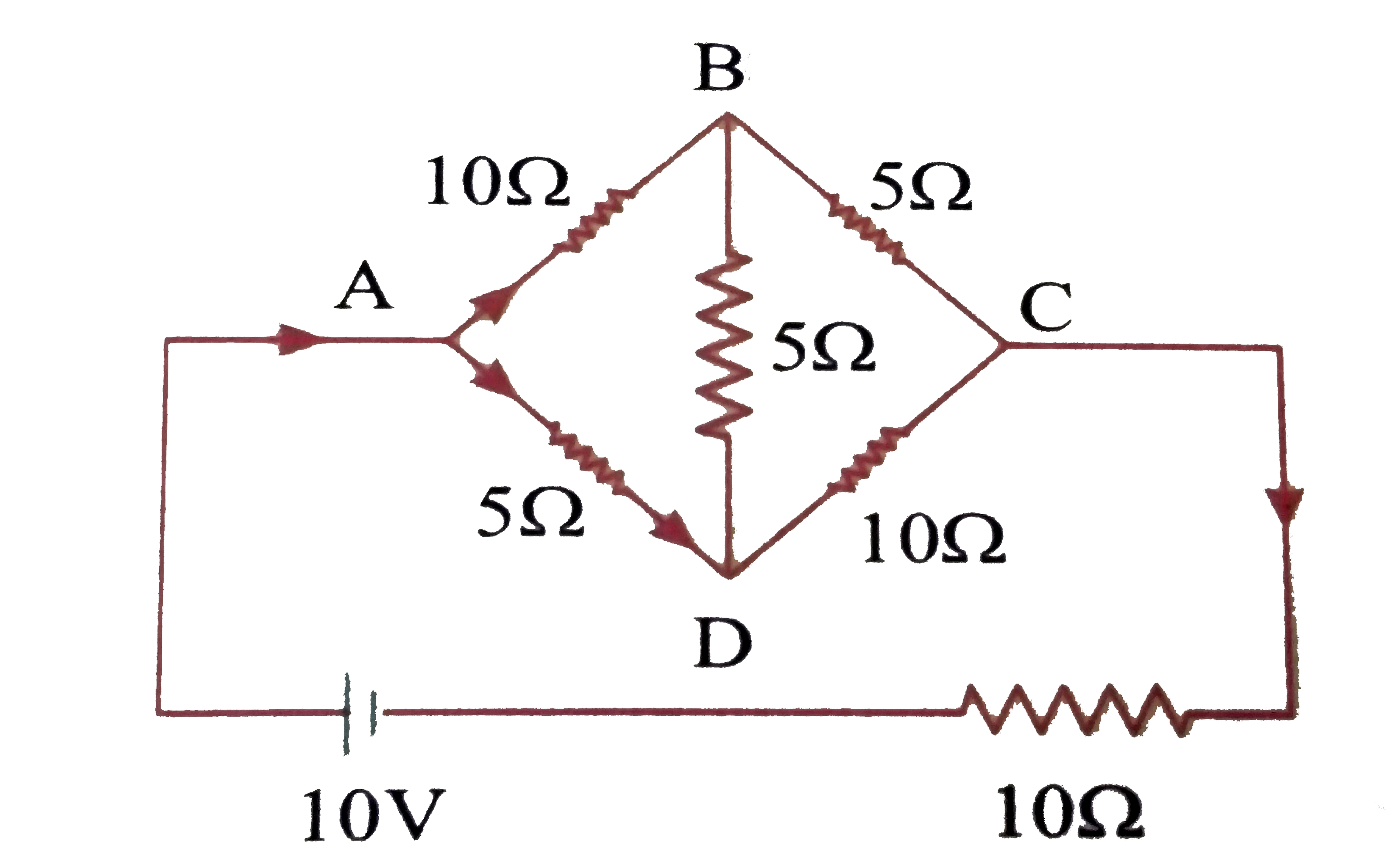
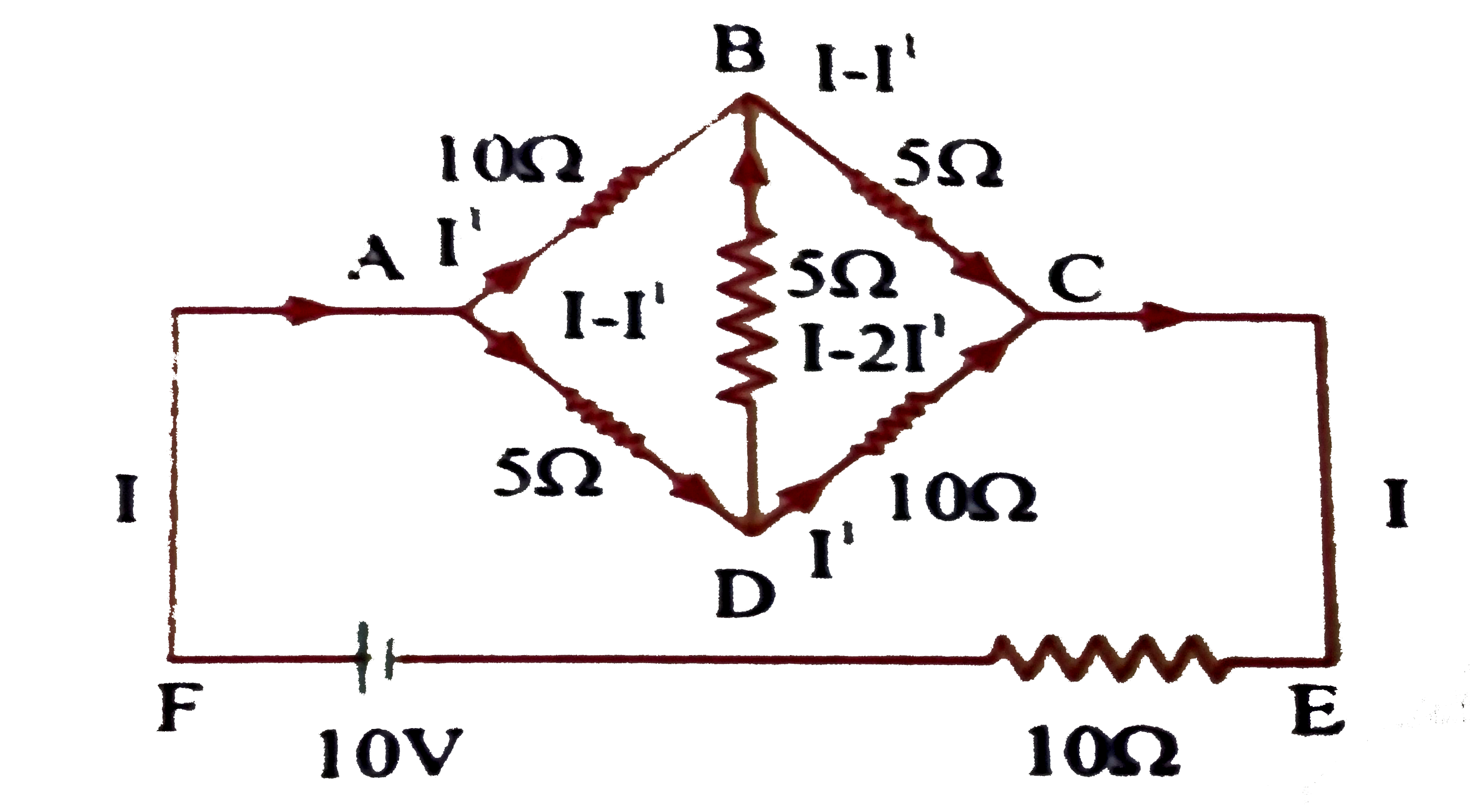
Determine the current in each branch of the network shown in fig.
View SolutionDetermine the current in each branch of the network shown in Fig.
View SolutionQuestions|Kirchhoff's Laws|Nodal Analysis
View Solution