A typical family car has four cylinders with a total cylinder volume of 1600 cm3 and a fuel consumption of 7.0 l per 100 km when driving at a speed of 90 km/h. During one second each cylinder goes through 25 burn cycles and consumes 0.4 g of fuel. Assume that fuel consists of 2 2 4-trimethylpentane C8H18.The compression ratio of the cylinder is 1:8. a Calculate the air intake of the engine m3/s. The gasified fuel and air are introduced into the cylinder when its volume is largest until the pressure is 101.0 kPa. Temperature of both incoming air and fuel are 100°C. Air contains 21.0 % by volume of O2 and 79.0 % of N2.It is assumed that 10.0 % of the carbon forms CO upon combustion and that nitrogen remains inert. b The gasified fuel and the air are compressed until the volume in the cylinder is at its smallest and then ignited. Calculate the composition % by volume and the temperature of the exhaust gases immediately after the combustion exhaust gases have not yet started to expand. The following data is given: Compound ∆Hf kJ/mol Cp J/mol K O2g 0.0 29.36N2g 0.0 29.13 COg -110.53 29.14 CO2g -395.51 37.11 H2Og241.82 33.58 2 2 4-trimethylpentane-187.82 c Calculate the final temperature of the leaving gases assuming that the piston has moved to expand the gases to the maximum volume of the cylinder and that the final gas pressure in the cylinder is 200 kPa. d To convert COg into CO2g the exhaust gases are led through a bed of catalysts with the following work function: nCO/nCO2 = 1/4 k [nCO/nCO2]1 Ve -t/towhere [nCO / nCO2]1 is the molar ratio before the catalyst v is the flow rate in mol/s and T the temperature of the gases entering the catalyst the same as the temperature of the leaving exhaust gases. T0 is a reference temperature 373 K and k is equal to 3.141 s/mol. Calculate the composition % by volume of the exhaust gases leaving the catalyst.
a MrC8H18 = 114.0 Cylinder volume V0 = 4.00 × 10-4 m3 p0 = 101 000 Nm-2 T0 = 373 K Considering one cylinder during one burn cycle one obtains f = fuel: mf = 0.400/25 g = 0.0160g nf = 1.4004 × 10-4 mol mf = mass of fuel nf = amount of substance of fuel nG = nf + nA = p0V0 / RT0 = 0.0130 mol nG = number of moles of gases nA = moles of air ⇒ nA = 0.0129 mol ⇒ Air intake of one cylinder during 25 burn cycles: VA = 25 nA R T0 / p0 = 9.902 ×10-3 m3 /s ⇒ The air intake of the whole engine is therefore: Vtotal = 4 VA = 0.0396 m3/s b The composition of the exhaust gases of one cylinder during one burn cycle is considered: before: Amounts of substances in mol before and after combustion: C8H18 O2COCO2 H2Obefore1.404 ×10-42.709 × 10-30 0 0after0 10.10 × 10-41.123 × 10-4 10.11 × 10-412.63 × 10-4The composition of the gas after combustion is therefore: Componen t N2 O2 COCO2H2O Total mol × 104101.9110.10 1.12 10.11 12.63 135.87 % 75.0 7.4 0.8 7.59.3 100 From thermodynamics the relation between the enthalpy and temperature change is given by c The final temperature of the leaving gases from one cylinder: p2 = 200 000 Pa V0 = 4.00 × 10-4 m3 nG = moles of exhaust gases in one cylinder = 0.01359 mol d The flow from all four cylinders is given: v = 4 × 25 × nG = 1.359 mol/s so that 0.01772 40.44 + x = 4.48 + x ⇒ x = 3.70 Thus the composition of the gas after the catalyst is:
Related Solutions
Carbon monoxide emitted by automobiles is an environmental hazard . A car has an engine of four cylinders with a total cylinder volume of 1600 cc and a fuel consumption fo 7.0 dm^(3) per 100 Km , when driving at an average speed of 80 km/hr . In one second , each cylinder goes through 25 burn cycles and consumes 0.400g of fuel . The compression ratio, which is the ratio between the smallest and largest volume within the cylinder as the piston moves forward and backward is 1:8. Calculate the air intake of the engine (m^(3)S^(-1)) , if the gaseous fuel and air are introduced into the cylinder when its volume is largest until the pressure is 101.0 KPa. the temperature of both incoming air and fuel is 100^(@) C. (Assume the fuel to be isoctane , C_(8)H_(18))
View SolutionCarbon monoxide emitted by automobiles is an environmental hazard . A car has an engine of four cylinders with a total cylinder volume of 1600 cc and a fuel consumption fo 7.0 per 100 Km , when driving at an average speed of 80 km/hr . In one second , each cylinder goes through 25 burn cycles and consumes 0.400g of fuel . The compression ratio, which is the ratio between the smallest and largest volume within the cylinder as the piston moves forward and backward is 1:8.
Calculate the air intake of the engine , if the gaseous fuel and air are introduced into the cylinder when its volume is largest until the pressure is 101.0 KPa. the temperature of both incoming air and fuel is C. (Assume the fuel to be isoctane ,
View SolutionCarbon monoxide emitted by automobiles is an environmental hazard . A car has an engine of four cylinders with a total cylinder volume of 1600 cc and a fuel consumption fo 7.0 per 100 Km , when driving at an average speed of 80 km/hr . In one second , each cylinder goes through 25 burn cycles and consumes 0.400g of fuel . The compression ratio, which is the ratio between the smallest and largest volume within the cylinder as the piston moves forward and backward is 1:8.
The gasified fuel and air are compressed to their lowest volume and then ignited .
The overall stoichiometric equation for the combustion reaction is
Calculate the temperature of the
i) gases just at the time of maximum compression and
ii) exhaust gases leaving the cylinder if the final pressure in the cylinder is 200 Kpa.
Relevant data needed for one burn cycle is given below.
View SolutionFuel present in gas cylinders is
View SolutionThe radius and height of a cylinder are in the ratio . If the volume of the cylinder is , find the total surface ara of the cylinder.
View SolutionThe radius and height of a cylinder are in the ratio 7:2. If the volume of the cylinder is 8316 cm^(3) ,find the total surface area of the cylinder.
View SolutionCalculate the total pressure in a 10 L cylinder which contains 0.4 g of helium, cylinder. Assume ideal behaviour of gases. (R=0.082 L atm K6(-1)mol^(-1))
View SolutionA metal cylinder of length L is subjected to a uniform compressive to a uniform compressive force F as shown in the figure. The material of the cylinder has Young's modulus Y and poisson's ratio sigma The change in volume of the cylinder is
View Solution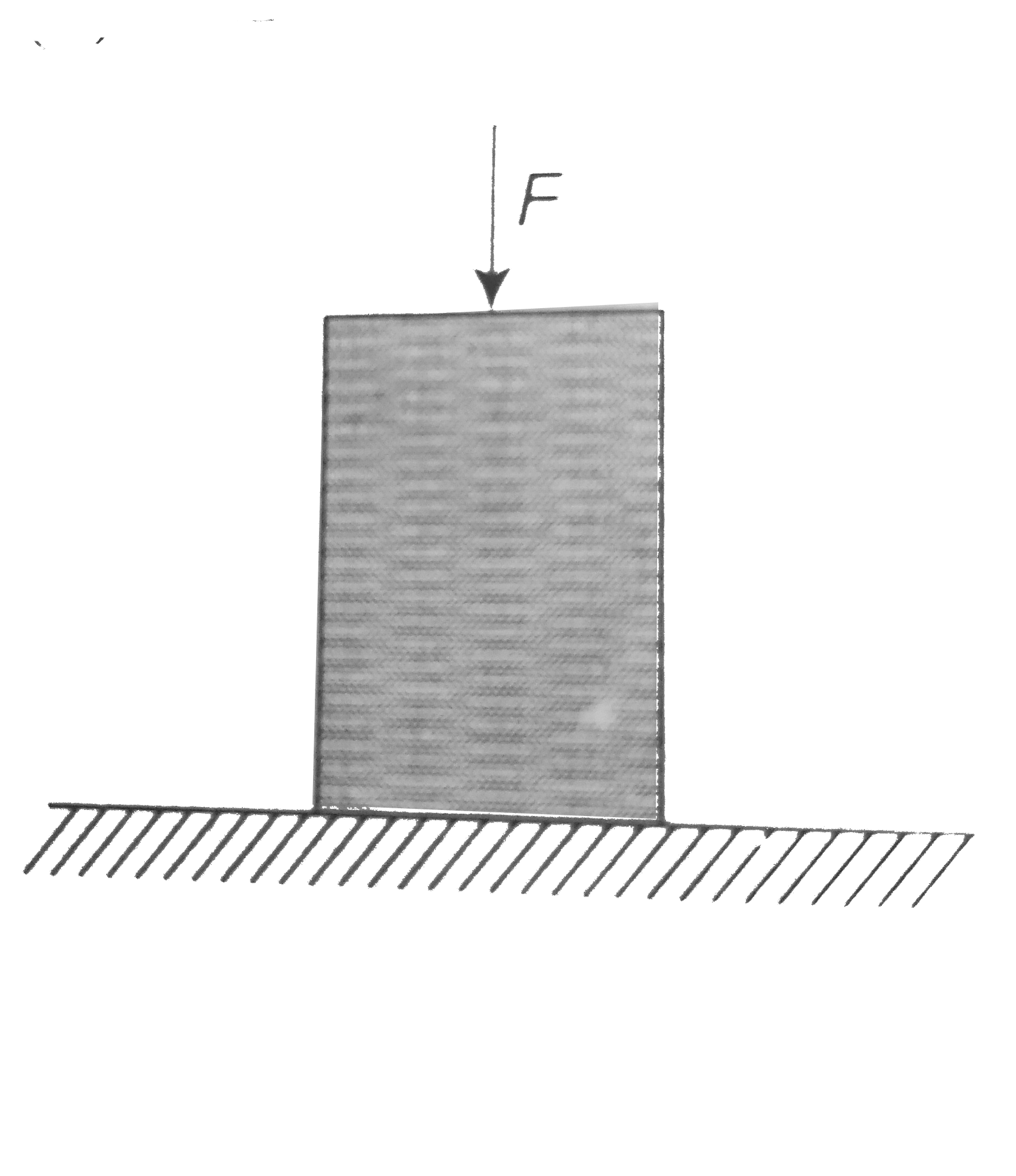
A metal cylinder of length is subjected to a uniform compressive to a uniform compressive force as shown in the figure. The material of the cylinder has Young's modulus and poisson's ratio The change in volume of the cylinder is
View SolutionCalculate the total pressure in a 10 L cylinder which contains g helium ,1.6 of oxygen and 1.4 g nitrogen at . Also calculate the partial of helium gas in the cylinder. Assume ideal hehaviour for gases.
View SolutionThe radii of the base of a cylinder and a cone are in the ratio 3 : 4 and their heights are in the ratio 2 : 3. The ratio of the volume of the cylinder to the volume of the cone is
View SolutionWe have container consists of 2 cylinder such that inner cylinder is a solid cylinder whose radius is and outer cylinder is a hollow cylinder whose radius is and height , the volume of fluid it can hold is
View SolutionA car covers 641 km in 43 litres of fuel. How much distance can this car cover in 1 litre of fuel?
View SolutionThe ratio of diameter and higher of a right circular cylinder is 4 : 7. The ratio of heights of cylinders is 5 : 2. What is the ratio of the volume of cylinder?
View SolutionThe total surface area of the solid cylinder is .If the area of the curved surface of the cylinder is one-third of the total surface area,then find the volume of the cylinder.
View Solutionसमान ऊँचाई वाले दो बेलनों की त्रिज्याओं में 1 : 3 का अनुपात है। पहले बेलन का आयतन 40 सेमी है। दूसरे बेलन का आयतन होगा
View Solutionदो समान ऊँचाइयों के बेलनों की त्रिज्याओं का अनुपात है। यदि पहले बेलन का आयतन 50 घन सेमी है, तो दूसरे बेलन का आयतन ज्ञात कीजिए।
View SolutionTwo thin planks are moving on a four identical cylinders as shown. There is no slipping at any contact points. Calculate the ratio of angular speed of upper cylinder to lower cylinder

View SolutionTwo thin planks are moving on a four identical cylinders as shown. There is no slipping at any contact points. Calculate the ratio of angular speed of upper cylinder to lower cylinder

View Solutionएक ठोस बेलन के सभी पृष्ठों का कुल क्षेत्रफल 924 है । यदि बेलन की त्रिज्या 7 सेमी है, तो बेलन का आयतन ज्ञात कीजिये।
View Solution