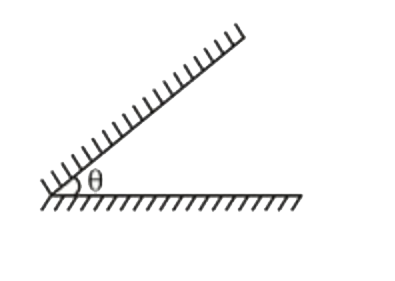
Two mirrors are inclined at an angle θ as shown in the figure. Light rays is incident parallel to one of the mirrors. Light will start retracing its path after third reflection if :A θ = 45ºB θ = 30ºC θ = 60ºD All three
Correct option B θ = 30º Explanation:90 – θ + θ = 90ºor θ = ϕ
Related Solutions
Two mirrors are inclined at angle as shown in figure. Light rays are incident parallel to one of mirrors. Light will start retracing its path after the reflection if

View SolutionTwo mirrors are inclined at angle theta as shown in figure. Light rays are incident parallel to one of mirrors. Light will start retracing its path after the reflection if
View SolutionTwo mirrors are inclined at angle theta as shown in figure. Light rays are incident parallel to one of mirrors. Light will start retracing its path after the reflection if
View Solutiontwo plane mirrors as shown in the figure theta is kept inclined at an angle. An incident light ray parallel to one of the mirrors will retrace its old path after the third reflection if -
View SolutionTwo mirrors are inclined at angle as shown in figure. Light rays are incident parallel to one of mirrors. Light will start retracing its path after the reflection if
View SolutionTwo plans mirrors are inclined to each other at some angle .A ray of light incident at on one,after reflection form the other retraces its path .The angles between the mirrors is:
View SolutionTwo plane mirrors are inclined at an angle theta . A ray of light incident parallel to one of them retraces its path back after successive reflections from the mirrors the value of theta is :
View SolutionTwo plane mirrors are inclined at an angle theta . A light ray incident on one of the mirrors undergoes multiple reflections. The angle of incidence on the first mirror is 15^@ . After reflection from the second mirror, if the light ray retraces its path, determine the value of theta.
View SolutionTwo plane mirror are inclined at an angle theta . A light ray incident on one of the mirror undergoes multiple reflections. The angle of incidence on the first mirror is 15^(@) . After reflection from the second mirror, if the light ray retraces its path, determine the volue of theta .
View Solution(1 + cot2 θ) (1 – cos θ) (1 + cos θ) = …………………. (a) tan2 θ – sec2 θ (b) sin2 θ – cos2 θ (c) sec2 θ – tan2 θ (d) cos2 θ – sin2 θ
View SolutionWhen two plane mirrors subtend an angle between them, then a ray of light incident parallel to one of them retraces its path afer n reflections such that (where c is constant)
If the angle between mirrors is . Then light ray retraces its path after n reflections where n is
View SolutionWhen two plane mirrors subtend an angle between them, then a ray of light incident parallel to one of them retraces its path afer n reflections such that (where c is constant)
If the angle between mirrors is . Then light ray retraces its path after n reflections where n is
View SolutionWhen two plane mirrors subtend an angle between them, then a ray of light incident parallel to one of them retraces its path afer n reflections such that (where c is constant)
If the angle between mirrors is . Then light ray retraces its path after n reflections where n is
View SolutionTwo plans mirrors are inclined to each other at some angle .A ray of light incident at 30^(@) on one,after reflection form the other retraces its path .The angles between the mirrors is:
View SolutionProve the identity (sin θ + cos θ)(tan θ + cot θ) = sec θ + cosec θ
View SolutionProve: sin θ(1 + tan θ) + cos θ(1 + cot θ) = (sec θ + cosec θ) .
View SolutionTwo plane mirrors are inclined to each other at a certain angle.A ray of light first incident on one of them at an inclination of 10^(@) with the mirror retraces its path after five reflections.The angle between the mirrors is
View SolutionIf sec θ + tan θ = 7, then evaluate sec θ – tan θ
View SolutionA ray of light is incident on a convex mirror as shown. Redraw the diagram and complete the path of this ray after reflection from the mirror. Mark angle of incidence and angle of reflection on it.
View SolutionFind the value of in
View Solution