If p is selected from the interval [0 5] then the probability that the equation 4x2 + 4px + p + 2 = 0 has real rootsa 1/2b 1/4c 3/5d 2/5
Correct option c 3/5Explanation:For real roots D ≥ 0⇒ p2– p – 2 ≥ 0⇒ p ≤ –1 p ≥ 2∴ p ∈ [2 5] but p ∈ [0 5]∴ required probability = 5 -2/5 - 0 = 3/5
Related Solutions
If p is chosen at random from the interval then the probability that the roots of the equation will be real is
View SolutionIf p is real, discuss the nature of the roots of the equation , in terms of p.
View SolutionIf an integer p is chosen at random in the interval , the probability that the roots of the equation are real , is
View SolutionStatement-1: If p is chosen at random in the closed interval [0,5], then the probability that the equation
has real is .
Statement-2: If discriminant , then roots of the quadratic equation are always real.
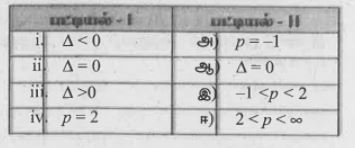
View Solutionபொருத்துக : சமன்பாடு க்கு.
View Solutionद्विघात बहुपद p(x) ज्ञात करें यदि एवं .
View SolutionIf and are the roots of the equation where ,p and q are real, then the roots of the equation are
View Solutionयदि p वास्तविक है तथा समीकरण p(x + 1) (x + 3) + 2 = 0 के मूल वास्तविक नहीं है , तो p का मान ज्ञात कीजिये।
View SolutionStatement-1: If p is chosen at random in the closed interval [0,5], then the probability that the equation
has real is .
Statement-2: If discriminant , then roots of the quadratic equation are always real.
View SolutionStatement-1: If p is chosen at random in the closed interval [0,5], then the probability that the equation
has real is .
Statement-2: If discriminant , then roots of the quadratic equation are always real.
View SolutionStatement-1: If p is chosen at random in the closed interval [0,5], then the probability that the equation
has real is .
Statement-2: If discriminant , then roots of the quadratic equation are always real.
View SolutionStatement-1: If p is chosen at random in the closed interval [0,5], then the probability that the equation
has real is .
Statement-2: If discriminant , then roots of the quadratic equation are always real.
View SolutionIF and are parallel find the value of p.
View Solutionदिया गया है तथा का वास्तविक मूल केवल x=0 है। यदि है, तो अंतराल [ -1,1] में
View SolutionLet Show that the equation has a unique root in the interval and identify it. (2001, 4M)
View SolutionLet- 1<=p<1 show that the equation 4x^(3)-3x-p=0 has a unique root in the interval [(1)/(2),1]
View SolutionIf one common root of the equations 3x^(2)+px+2=0 and -3x^(2)+qx+2=0 is alpha and product of other roots of equations is -1, then (a)p=5,q=-1(b)p=-5,q=-1(c)q=1,p=-5 (d) q=1,p=5
View SolutionGiven P(x)=x^(4)+ax^(3)+ + bx^(2)+cx+d such that x =0 is the only real root of p'' (x)=0 . If P(-1) lt P(1) , then in the interval [-1, 1] :
View SolutionIf a variable takes the discrete values p+4,p-(7)/(2),p-(5)/(2),p-3,p-2,p+(1)/(2),p-(1)/(2),p+5,p>0 then the median is.
View Solutiona^(2)+b^(2)+4c^(2)=2a+2b-4c+3=0
View Solution