Consider a line l with equation ax + by + c = 0. Show that the expression ax1 + by1 +c is positive for x1 y1 on one side of the line l and negative for all points on the other side.
Note that a point x1 y1 lies on the line l if and only if ax1 +by1 +c = 0.Suppose that points α β and γ δ are on the same side of l. Then the line segment from α β and γ δ does not cross l. So ax1 + by1 + c≠ 0 for each point x1 y1 on the line segment. Thus the expression ax1 + by1 + c cannot change sign as the point x1 y1 moves along the line segment from α β to γ δ. Hence the signs of aα + bβ + c and aγ + bδ + c are the same. Points on different sides of l must have different signs as it is possible to choose x1 y1 so that ax1 + by1 + c > 0 and choose x2 y2 so that ax2 + by2 + c < 0.
Related Solutions
বিন্দুগামী কোন সরলরেখা - এর নতিমাত্রা ঋণাত্মক | রেখাটি অক্ষ দুটির ধনাত্মক দিকে যথাক্রমে ও বিন্দুতে ছেদ করে | মূলবিন্দু হলে, পরিবর্তনশীল -এর জন্য -এর ক্ষুদ্রতম মান হবে-
View Solutionসরলরেখা এমনভাবে গতিশীল যে তার সব অবস্থানে । দেখাও যে সরলরেখাটি একটি স্থির বিন্দুগামী এবং ওই বিন্দুর স্থানাঙ্ক নির্ণয় করো।
View Solutionयदि वर्ग समीकरण का एक मूल धनात्मक है और दूसरा ऋणात्मक तन ऐसा होने के लिए क्या प्रतिबन्ध है ?
View SolutionFind the locus of the circumcenter of a triangle whose two sides are along the coordinate axes and the third side passes through the point of intersection of the line and
View SolutionFind the locus of the circumcenter of a triangle whose two sides are along the coordinate axes and the third side passes through the point of intersection of the line a x+b y+c=0 and l x+m y+n=0.
View SolutionFind the locus of the circumcenter of a triangle whose two sides are along the coordinate axes and the third side passes through the point of intersection of the line a x+b y+c=0 and l x+m y+n=0.
View Solutionদেখাও যে, x অক্ষের ধনাত্মক দিকের সঙ্গে কোনে নত সরলরেখার সমান্তরাল দিকে পরিমিত বিন্দু থেকে সরলরেখা দূরত্ব হয়, ।
View SolutionIf the mean of n observations ax1, ax2, ax3, ...., axn is aX show that (ax1-aX) + (ax2-aX) + .....+ (axn - aX) = 0
View SolutionIf the mean of n observations ax1, ax2, ax3, ...., axn is aX show that (ax1-aX) + (ax2-aX) + .....+ (axn - aX) = 0
View SolutionProve that the incentre of the triangle whose vertices are given by A(x1,y1),B(x2,y2),C(x3,y3)is(ax1+bx2+cx3)/(a+b+c),(ay1+by2+cy2)/(a+b+c) where a b,and c are the sides opposite to the angles A,B and C respectively.
View SolutionThe point C is the image of point A in line l and line segment BC intersects the line l at P.
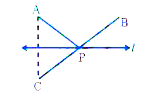
Is the image of P in line l the point P itself ?
View SolutionIn the equations if one roots is negative of the other then:
View SolutionIf the lines joining the origin to the points of intersection of a line L and are coordinate axes then equation of L is
View SolutionIf 3a +2b+c=0 for all positions of the moving line ax+by+c=0 , show that the line always passes through a fixed point . Find the coordinates of that fixed point.
View SolutionIf a+b+c=0 for all positions of the moving line ax+by+c=0 , show that the line always passes throught a fixed point . Find the coordinates of that fixed point.
View Solutionमाना रेखा है पर अक्षों द्वारा
रेखा पर अक्षों द्वारा काटे गए अंतः खण्डों का मध्य बिंदु का बिंदुपथ होगा
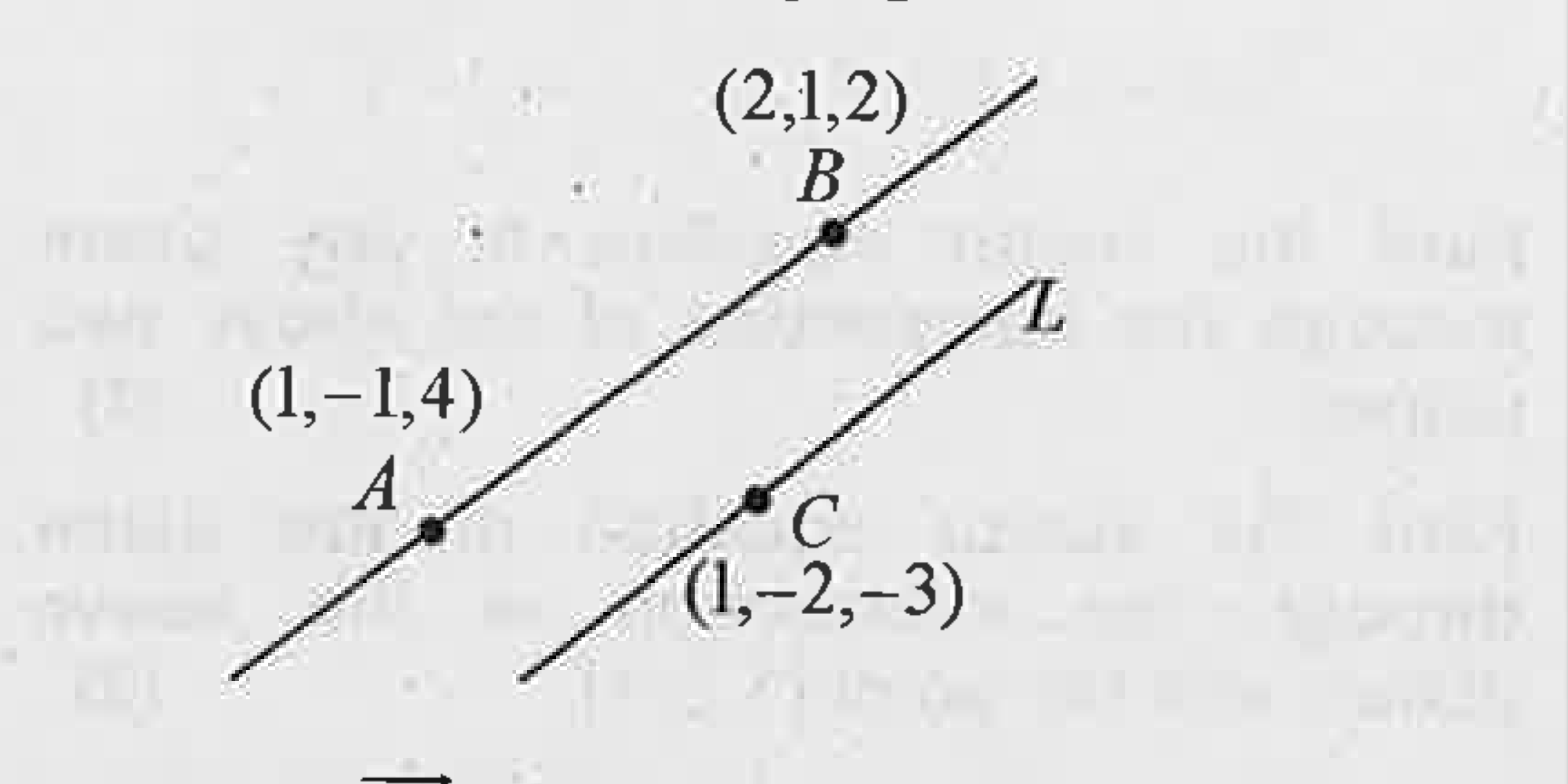
View SolutionFrom the following figure
Find a point on line L other than C.
View Solutionবিন্দুগামী কোন সরলরেখা - এর নতিমাত্রা ঋণাত্মক | রেখাটি অক্ষ দুটির ধনাত্মক দিকে যথাক্রমে ও বিন্দুতে ছেদ করে | তলে একটি চলমান বিন্দু এমনভাবে গতিশীল যে একটি আয়তাকার উৎপন্ন হয় | পরিবর্তনশীল হলে, -এর সঞ্চারপথ হবে-
View SolutionConsider two points A and B and a line L as shown in figure.
Find the Cartesian equation of the line L.
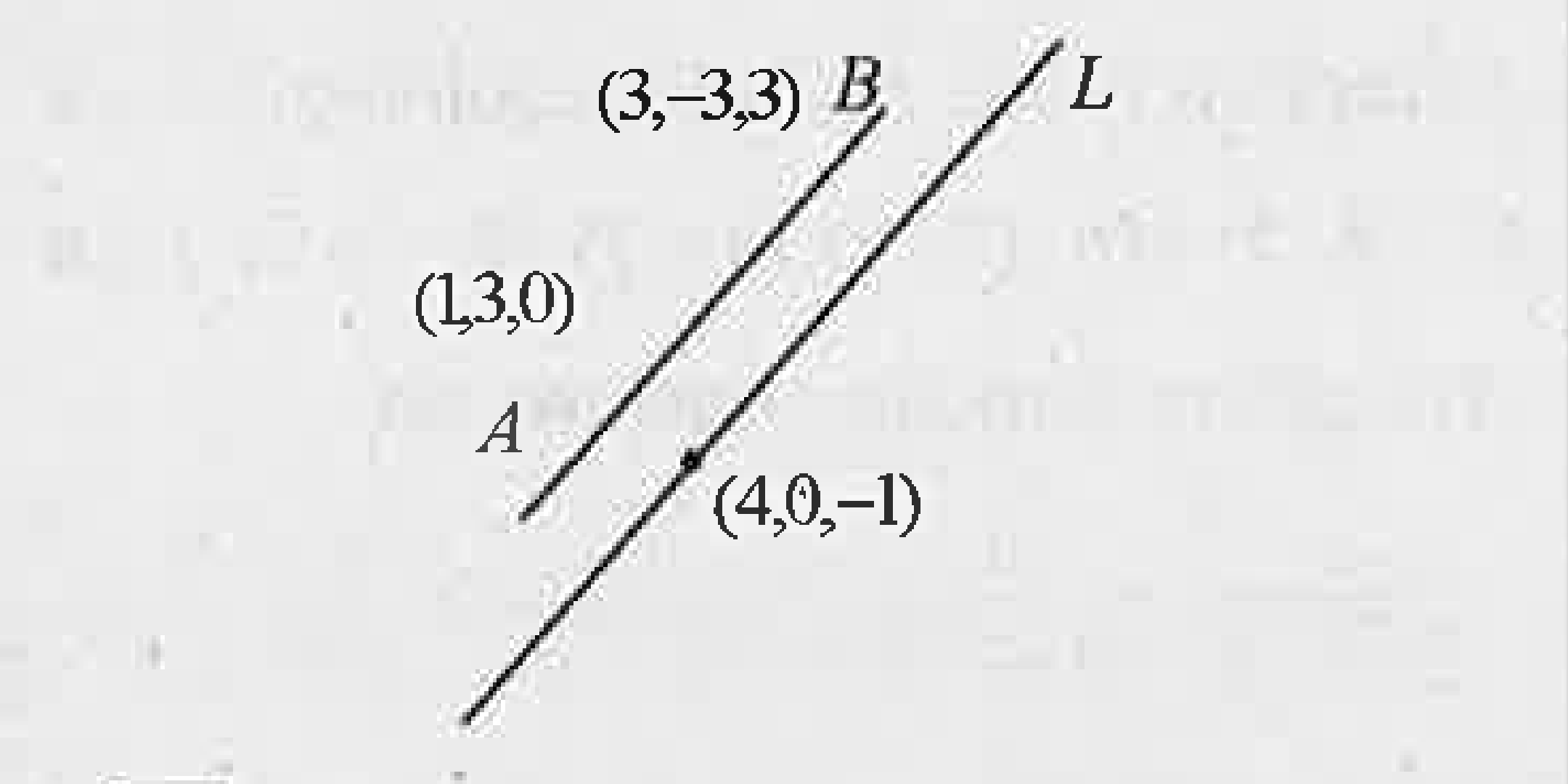
View SolutionThe point C is the image of point A in line l and line segment BC intersects the line l at P.
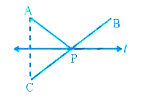
Is PA = PC ?
View Solution