Suppose points A B and C are not collinear and have coordinates x1 y1 x2 y2 and x3 y3. Let D be the midpoint of BC and suppose G divides the median AD in the ratio 2 : 1. Find the coordinates of G and deduce that the medians of 4ABC are concurrent.
The midpoint D of BC isx2 + x3/2 y2 + y3/2The point G that divides the median AD in the ratio 2 : 1 isThis is symmetric in x1 x2 x3 and in y1 y2 y3. So G lies on the other medians BE and C F and the medians are concurrent.
Related Solutions
-কে একটি তৃতীয় ক্রমের নির্ণায়কের আকারে লিখলে তা হবে-
View Solutionযদি a একক বাহুবিশিষ্ট সমবাহু ত্রিভুজের তিনটি শীর্ষ এবং হয় তবে প্রমাণ করো যে,
View SolutionThe co-ordinates of the vertices are A(x1,y1)B(x2,y2) and C(x3,y3). The line joining the points A and B is divided by a point P in the ratio 1:k and line joining by a point P in the point Q in the ratio m:k+1. Find co-ordinates of Q.
View SolutionAD is the median on BC. Find the coordinates of the point D
View SolutionAD is the median on BC. Find the coordinates of the point D
View SolutionAD is the median on BC. Find the coordinates of the point D
View Solution(b)The coordinates of the point R which divides the line segment joining P(x1,y1,z1) and Q(x2,y2,z2) internally in the ratio m:n are given by…………
View SolutionLet A (4, 2), B(6, 5) and C(1, 4) be the vertices of . AD is the median on BC. Find the coordinates of the point D.
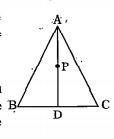
View SolutionLet A(4,2) , B(6,5) and C(1,4) be the vertices of the . The median from A meets BC at D. Find the coordinates of the point D. Find the coordinates of the point P on AD such that AP : PD = 2 : 1 .
View Solutionके शीर्ष A, B और C के निर्देशांक क्रमशः और है | यदि BC का मध्यबिंदु D हो तो माधिका AD की लम्बाई ज्ञात कीजिय|
View SolutionIn , D is the midpoint of seg MN. If , find the coordinates of the point G which divides the median internally in the ratio
View SolutionLet (4, 2), B (6, 5) and C (1, 4) be the vertices of . :- The median from A meets BC at D. Find the coordinates of the point D.
View SolutionProve that the incentre of the triangle whose vertices are given by A(x1,y1),B(x2,y2),C(x3,y3)is(ax1+bx2+cx3)/(a+b+c),(ay1+by2+cy2)/(a+b+c) where a b,and c are the sides opposite to the angles A,B and C respectively.
View SolutionThe number of integral solution of x1+x2+x3+x4=25, such that x1>=1,x2>=2,x3>=3,x4>=4
View SolutionIf a x1 2+b y1 2+c z1 2=a x2 2+b y2 2+c z2 2=a x3 2+b y3 2+c z3 2=d ,a x2 3+b y_2y_3+c z_2z_3=a x_3x_1+b y_3y_1+c z_3z_1=a x_1x_2+b y_1y_2+c z_1z_2=f, then prove that |x_1y_1z_1x_2y_2z_2x_3y_3z_3|=(d-f){((d+2f))/(a b c)}^(1//2)
View SolutionThe coordinates of points A, B and C are . Verify if the medians of the triangle ABC are concurrent..
View SolutionThe coordinates of points A, B and C are . Verify if the medians of the triangle ABC are concurrent..
View Solutionand are the vertices of . The median from meets in . Find the coordinates of the point .
View SolutionIf is the mean of x1, x2,x2,x3, ………..xn , then the mean of x1+a,x2+a, x3+a...xn+a
View Solutionमान लीजिये A(4,2), B(6,5) और C(1,4) एक त्रिभुज ABC के शीर्ष है।
A से होकर जाने वाली मध्यिका BC से D पर मिलती है। बिंदु D के निर्देशांक ज्ञात कीजिये।
View Solution