If vectora b c d are four distinct vectors satisfying the conditions vectora x b = vectorc x d and vectora x c = vectorb x d then prove that vectora x b + c x d ≠ a x c + b x d.
Given vectora x b = vectorc x d
Related Solutions
The value of x^d/(x^d + x^(d+b -a)+x^(d+c-a))+(x^d)/(x^d + x^(d+a-b)+x^(d+c-b))+(x^d)/(x^d+x^(d+a-c)+x^(d+b-c)) is
View Solutionif a,b,c and d are distinct integers such that a+b+c+d=17, then the real roots of (x-a)(x-b)(x-c)(x-d)=4 are
View SolutionIf =x^3,then the equation having
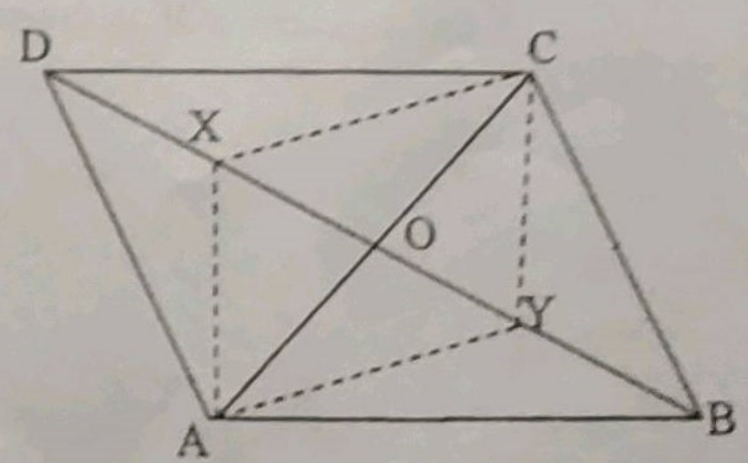
View SolutionIn Figure, is a parallelogram and are points on the diagonal such that . Prove that is a parallelogram (ii) (iv)
View SolutionIn Figure, is a parallelogram and are points on the diagonal such that . Prove that is a parallelogram (ii) (iv)
View Solution
View Solution((x-a)(x-b))/((x-c) (x-d)) = (A)/(x-c) - (B)/((x-d)) +C , Then C =
View SolutionIn a median is produced to such that . Prove that is a parallelogram.
View SolutionIn a median is produced to such that . Prove that is a parallelogram.
View SolutionIf , then show that and are in G.P.
View SolutionIf then is equal to (a) (b) (c) (d)
View SolutionIf then the least value of the function, (b) (d)
View SolutionIf then a, b, c, d are in
View SolutionIf then is equal to
View SolutionIf then is equal to (a) (b) (c) (d)
View SolutionIf (cosx)/a=(cos(x+theta))/b=(cos(x+2theta))/c=(cos(x+3theta))/d then (a+c)/(b+d) is equal to (a) a/d (b) c/b (c) b/c (d) d/a
View SolutionIf then is equal to (a) (b) (c) (d)
View SolutionIn a triangle median is produced to such that Prove that is a parallelogram.
View SolutionIn a triangle median is produced to such that Prove that is a parallelogram.
View SolutionIn a triangle median is produced to such that Prove that is a parallelogram.
View Solution