Prove that the rectangle circumscribing a circle is a square.
AP = AS BP= BQ CR= CQ and DR= DS⇒AP + BP + CR + DR = AS + BQ + CQ + DSQ ⇒ AB + CD = AD + CBBut AB = CD and AD = CB∴ AB = ADHence ABCD is a square.
Related Solutions
Prove that the rectangle circumscribing a circle is a square
View SolutionProve that the rectangle circumscribing a circle is a square
View SolutionIf a rectangle be circumscribed about a circle prove that it is a square.
View SolutionA rectange circumscribing a circle is a square.
View SolutionProve that ,the greatest rectangle inscribed in a given circle is a square.
View Solutionसिद्ध कीजिए कि वृत्त के अंतर्गत महत्तम क्षेत्रफल वाला आयत एक वर्ग है
View SolutionA circle circumscribes a rectangle with sides 16cm and 12cm. What is the area of the circle
View SolutionA square is circumscribed about a circle which is turn circumscribes another square. The ratio of the area of outer square to the inner square
View SolutionA square is circumscribed about a circle which is turn circumscribes another square. The ratio of the area of outer square to the inner square
View SolutionA circle is circumscribed about a square. If the side of the square be 5 cm, then the diameter of the circle is
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
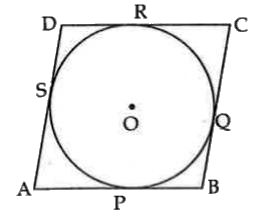
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a Rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
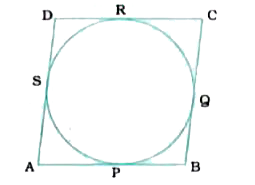
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View Solution