In a ∆ ABC BC = 2 CA = 1 + √3 and ∠C = 60°. Feet of the perpendicular from A B and C on the opposite sides BC CA and AB are D E and F respectively and are concurrent at P. Now match the entries of Column I with respective entries of Column II.Column IColumn IIARadius of the circle circumscribing the ∆DEF is p√6 - √2/4BArea of the ∆ DEF isq1/√2CRadius of the circle inscribed in the ∆ DEF isr√3/4s√6 + √2/4
Correct option A →q; B → r; C →p; D →qExplanation:CA = b = 1 + √3BC = a = 2 cosC = 1/2∆DEF is pedal triangle of ∆ABC∠DEB = π/2 - A ⇒ ∠DEF = π - 2AA Circum scribing circle = EF/sinEDF
Related Solutions
In a . Feet of the perpendicular from A, B and on the opposite sides BC, CA and AB are D, E and F respectively and perpendiculars are concurrerant at P.
Now match the entries of Column-I with respective entries of column-II.
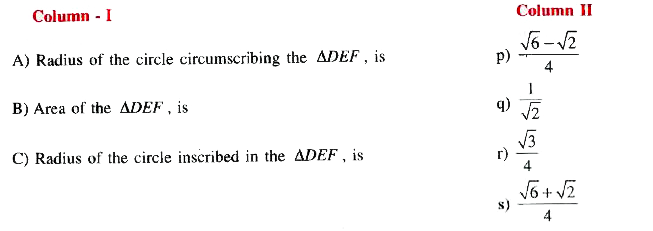
View SolutionABC ত্রিভুজের AB, BCও CA বাহুর মধ্যবিন্দুগুলি যথাক্রমে D, E ও F। প্রমাণ করো, ।
View Solutionలో AB,BC మరియు CA భుజాల మద్య బిందువులు వరుసగా D, E మరియు F లు అయిన =
View SolutionA triangle with BC = a, CA = b, AB = c is a measure of the semicircle of ABC. A circle triangle ABC Touch the sides BC, CA, AB in D, E, F respectively, then prove that BD = s - b .
View SolutionD, E and F are the midpoints of triangles ABC BC, CA and AB respectively. ar (DEF) =1/4 ar (ABC)
View SolutionIn a Δ ABC, D,E,F are respectively, the mid- points of BC,CA, and AB. If the lengths of side AB, BC and CA are 7 cm, 8 cm, 9 cm, respectively, find the perimeter of Δ DEF.
View SolutionLet's denote the semi-perimeter of a triangle ABC in which BC = a, CA = 5, AB = c. If a circle touches the side BC, CA, AB at D, E, F respectively, prove that BD = S-b.
View Solutionत्रिभुज ABC की भुजाओं BC, CA तथा AB के मध्य बिन्दु क्रमश: D, E, F है, तो त्रिभुज DEF के केन्द्रक का स्थित सदिश होगा, जबकि A, B, C के स्थिति सदिश क्रमश है-
View SolutionIf D,E and F are respectively the midpoint of the sides BC,CA and AB of a Delta ABC and the area of Delta ABC = 36 m^2 , then area of Delta DEF is -----
View SolutionD,E,F are the foot of the perpendiculars from vertices A,B,C to sides BC,CA,AB respectively,and H is the or the centre of acute angled triangle ABC, where a,b,c are the sides of triangle ABC, then
View SolutionThe in circle of touches the sides BC, CA and AB at D, E and F respectively. Then AF + BD + CE is equal to :
View SolutionLet the incircle of a touches sides BC, CA and AB at D,E and F, respectively. Let area of be and thatof DEF be . If a, b and c are side of , then the value of is
View SolutionIf D, E and F are the mid-points of sides BC, CA and AB respectively of , then the ratio of the areas of to the area of is :
View Solutionలో BC,CA, AB భుజాల మధ్యబిందువులు వరుసగా D, E, ఫ। అయిన మరియు ల వైశాల్యాల నిష్పత్తిని కనుగొనండి.
View SolutionD, E and F are respectively the mid-points of sides AB, BC and CA of . Find the ratio of the areas of .
View Solutionएक त्रिभुज ABC कि भुजाओ AB, BC और CA के मध्य-बिंदु क्रमशः D,E और F है और के क्षेत्रफलों का अनुपात ज्ञात कीजिए
View SolutionD,E,F are the mid points of the sides BC, CA and AB respectively of a . Determine the ratio of the areas of and .
View SolutionD.E और F क्रमशः की भुजाओं के मध्य बिंदु है, तो = ?
View SolutionD, E and F are the mid-points of the sides BC, CA and AB of the triangle ABC respectively. show that ar (Delta DEF) = (1)/(4) ar (DeltaABC)
View SolutionLet s denote the semi-perimeter of where , and . If a circle touches the sides BC, CA, and AB at D, E, and F respectively, prove that .
View Solution