The triangle ABC with side lengths a b c as usual satisfies loga2 = logb2 + logc2 - log2bc cosA. What can you say about this triangle?
a2 = b2c2/2bcosAcosA = bc/2a2 = b2 + c2 - a2/2bc⇒ b2c2 = a2b2 + a2c2 – a4⇒ b2c2 – a2 – a2c2 – a2 = 0⇒ c2 – a2b2 – a2 = 0⇒ either c = a or a = bHence triangle is isosceles.
Related Solutions
The triangle ABC (with side lengths a b,cas usuall satisfies log a^(2)=log b^(2)+log c^(2)-log(2bc cos A) What can you say about this triangle?
View SolutionWhat can you say about the set, A,B,if
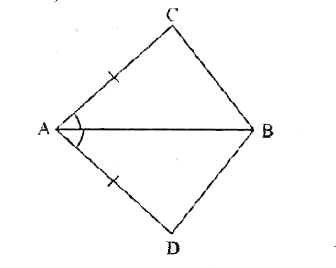
View SolutionAC = AD and AB biseets A. show that . What can you say about BC and BD?
View SolutionIn a , with usual notations , prove that .
View SolutionIf the circumcentre and the incentre of a triangle coincide, then what can you say about the triangle ?
View Solution.
View SolutionIf in cosA/cosB =a/b then is
View SolutionIn Delta ABC measure of angle B is 900. If cosA = 5/13, and AB = 10cm, then what is the length (in cm) of side BC?
View Solutionযে কোনো ত্রিভুজের -তে ভেক্টর পদ্ধতির প্রয়োগে প্রমান করো যে, , যেখানে ত্রিভুজের কোণের বিপরীত বাহুর দৈর্ঘ্য যথাক্রমে ।
View SolutionIf the length of the sides of the triangle ABC satisfy, , then triangle ABC is:
View SolutionIn a triangle ABC, if (cosA)/a=(cosB)/b=(cosC)/c and the side a =2 , then area of triangle is
View SolutionIn a triangle ABC, if (cosA)/a=(cosB)/b=(cosC)/c and the side a =2 , then area of triangle is
View SolutionIn triangle ABC, a, b, c are the lengths of its sides and A, B C are the angles of triangle ABC. The correct relation is
View SolutionIn triangle ABC, a, b, c are the lengths of its sides and A, B, C are the angles of triangle ABC. The correct relation is given by
View SolutionIf in a triangle ABC, ,then the triangle is
View SolutionIf in a triangle ABC, ,then the triangle is
View SolutionIf in a triangle ABC, ,then the triangle is
View Solutionयदि है तो त्रिभुज ABC की भुजाये है
View Solutionयदि त्रिभुज ABC में और a =2 हो, तो त्रिभुज ABC का क्षेत्रफल ज्ञात कीजिए ।
View SolutionThe lengths of the sides of △ABC are consecutive integers. In △ABC has the same perimeter as an equilateral triangle triangle with a side of length 9cm, what is the length of the shortest side of △ABC?
View Solution