The product of the distances of the in centre from the angular points of a ∆ABC isA 4R2rB 4Rr2C abcR/sD abcs/R
Correct option B 4Rr2Explanation:
Related Solutions
In , x , y , and z are the distance of incentre from angular points A , B ,and C respectively . If , then =
View SolutionIn , x , y , and z are the distance of incentre from angular points A , B ,and C respectively . If , then =
View SolutionThe product of the distances of the incentre from the angular points of a is
View SolutionAL, BM and CN are perpendicular from angular points of a triangle ABC on the opposite sides BC, CA and AB respectively. is the area of triangle ABC, (r ) and R are the inradius and circumradius.
Radius is the circum circle of is
View SolutionThe distance of the incentre of the triangle ABC from A is
View SolutionThe orbital angular momentum of a satellite revolving at a distance r from the centre is L . If the distance is increased to 16r , then the new angular momentum will be
View SolutionThe orbital angular momentum of a satellite revolving at a distancer from the centre is L. If the distance is
increased to 16 r, then new angular momentum will be
View SolutionAD,BE and CF are the perpendiculars from the angular points of a Delta ABC upon the opposite sides.The perimeters of the Delta DEF and Delta ABC are in the ratio-
View SolutionLet O be the in-centre of a triangle ABC and D be a point on the side BC of , such that If , then
View SolutionAL, BM and CN are perpendicular from angular points of a triangle ABC on the opposite sides BC, CA and AB respectively. is the area of triangle ABC, (r ) and R are the inradius and circumradius.
If perimeters of then the value of is
View SolutionAL, BM and CN are perpendicular from angular points of a triangle ABC on the opposite sides BC, CA and AB respectively. is the area of triangle ABC, (r ) and R are the inradius and circumradius.
If perimeters of then the value of is
View SolutionAL, BM and CN are perpendicular from angular points of a triangle ABC on the opposite sides BC, CA and AB respectively. is the area of triangle ABC, (r ) and R are the inradius and circumradius.
If perimeters of then the value of is
View SolutionABC is a triangle. Locate a point in the interior of ABC which is equidistant from all the vertices of ABC
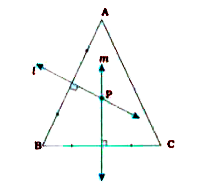
View SolutionABC is a triangle. Locate a point in the interior of which is equidistant from all the vertices of
View SolutionABC is triangle. Locate a point in the interior of ABC which is equidistant from all the vertices of .
View SolutionThe orbital angular momentum of a satellite revolving at a distance r from the centre is L. If the distance is increased to 16 r then new angular momentum will be
View SolutionThe orbital angular momentum of a satellite revolving at a distance r from the centre is L . If the distance is increased to 16 r, then the new angular momentum will be
View SolutionThe orbital angular momentum of a satellite revolving at a distance r from the centre is L . If the distance is increased to 16 r, then the new angular momentum will be
View SolutionIf spheres of radius 'r' are arranged in ccp fashion (ABC ABC…) the vertical distance between any two consecutive A layers is
View SolutionIf spheres of radius 'r' are arranged in ccp fashion (ABC ABC…) , the vertical distance between any two consecutive A layers is
View Solution