Two wires A and B have the same length and area of cross section. But Young’s modulus of A is two times the Young’s modulus of B. Then the ratio of force constant of A to that of B isa 1b 2c 1/2d √2
Correct option b 2Explanation:Force constant of wire
Related Solutions
Two wires A and B have the same length and area of cross-section. But Young's modulus of A is two times the Young's modulus of B. Then the ratio of force constant of A to that of B is
View SolutionTwo wires A and B have the same length and area of cross-secton. But Young's modulus of A is two times the Young's modulus of B. Then the ratio of force constant of A to that of B is
View SolutionTwo wires A and B have the same length and area of cross-secton. But Young's modulus of A is two times the Young's modulus of B. Then the ratio of force constant of A to that of B is
View SolutionTwo wires A and B have the same length and area of cross section. But young's modulus of A is two times the young's modulus of B. Then what is the ratio of force constant of A to that of B?
View SolutionTwo wires A and B have the same length and cross section. But Young's modulus of elasticity of A is twice the Young's modulus of elasticity of B. Then the ratio of the force constants of A and B will be
View SolutionA steel wire of length 4.7 m and cross-sectional area stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of under a given load. What is the ratio of the Young’s modulus of steel to that of copper?
View SolutionA steel wire of length 4.7 m and cross-sectional area stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of under a given load. What is the ratio of the Young’s modulus of steel to that of copper?
View SolutionA elongation of 0.1% in a wire of cross-sectional area 10"6 m2 causes tension 100 N. The young’s modulus is
View SolutionIf the temperature of the wire is increased, then the Young’s modulus will
View SolutionTwo wires have identical lengths and areas of cross-section are suspended by mass M . Their Young's modulus are in the ratio 2:5 .
View SolutionTwo wires have identical lengths and areas of cross-section are suspended by mass M . Their Young's modulus are in the ratio 2:5 .
View SolutionA wire of length l, area of cross section A and Young’s modulus of elasticity Y is stretched by a longitudinal force F. The change in length is Match the following two columns.
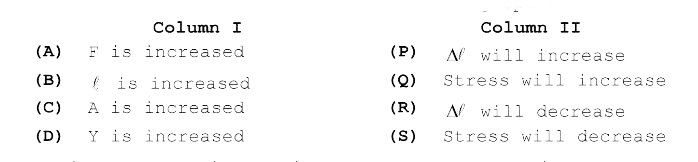
View SolutionA wire of length l, area of cross section A and Young’s modulus of elasticity Y is stretched by a longitudinal force F. The change in length is Deltal Match the following two columns.
View SolutionA brass wire of length 4.5m with cross-section area of and a copper wire of length 5.0 m with cross section area are stretched by the same load. The same elongation is produced in both the wires. Find the ratio of Young’s modulus of brass and copper.
View SolutionWhat is Young’s modulus? Describe an experiment to find out Young’s modulus of material in the form of a long string wire.
View SolutionThe Young’s modulus of a wire is numerically equal to the stress which will:
View SolutionThe temperature of a wire is doubled. The Young’s modulus of elasticity will
View SolutionTwo wire A & B are of the same metal and are of same length have area of cross section in the ratio of 2:1 If the same potential difference is applied across each wire. What will be the ratio of the current flowing through the wires A & B ?
View SolutionTwo wire A & B are of the same metal and are of same length have area of cross section in the ratio of If the same potential difference is applied across each wire. What will be the ratio of the current flowing through the wires A & B ?
View SolutionTwo copper wires A and B of length l and 2l respectively, have the same area of cross-section. The ratio of the resistivity of wire A to the resistivity of wire B is
View Solution