If A3 4 and C1 −1 are the ends of a diagonal of a square ABCD then find the equations of the sides of the square.
See Fig.Equation of the line AC isy - 4 = 4 + 1/3 - 1x - 32y - 8 = 5x - 155x - 2y - 7 = 0 Its slope is 5/2. Let the slope of side CD be m. Then Therefore equations of CB and CD are Similarly the equations of AB and BD respectively are Therefore the equations of the sides are 3x − 7y − 10 = 0 7x + 3y − 4 = 0 3x − 7y − 19 = 0 and 7x + 3y − 33 = 0 Aliter Using Complex Numbers: Let A = 3 + 4i C = 1 − i M = midpoint of AC = 2 + 3/2i. Let B denote Z. Rotate barMA about M through 90° in the anticlockwise sense so that Now we can write the sides equations because the vertices are obtained as A3 4 B−1/2 5/2 C1 −1 D9/2 1/2.
Related Solutions
ABCD is a square. Find the side of the square.
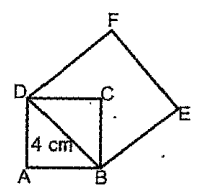
View SolutionABCD is a square. Its diagonal = 4 cm. BDFE is a square.
Find the area of ABCD
View SolutionIf the extrremities (end points) of a diagonal of a square are (1,-2,3) and (2,-3,5) then find the length of the side of square.
View SolutionOne side of a square is inclined to the x-axis at an angle and one of its extremities is at the origin. If the side of the square is , find the equations of the diagonals of the square.
View SolutionOne side of a square is inclined to the x-axis at an angle and one of its extremities is at the origin. If the side of the square is 4, find the equations of the diagonals of the square.
View SolutionABCD is a square. Find out the side of square?
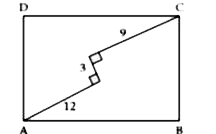
View SolutionIf the sum of the lengths of two diagonals of the given square ABCD is 24 cm, then find the side of the square and the magnitude of AO + OB.
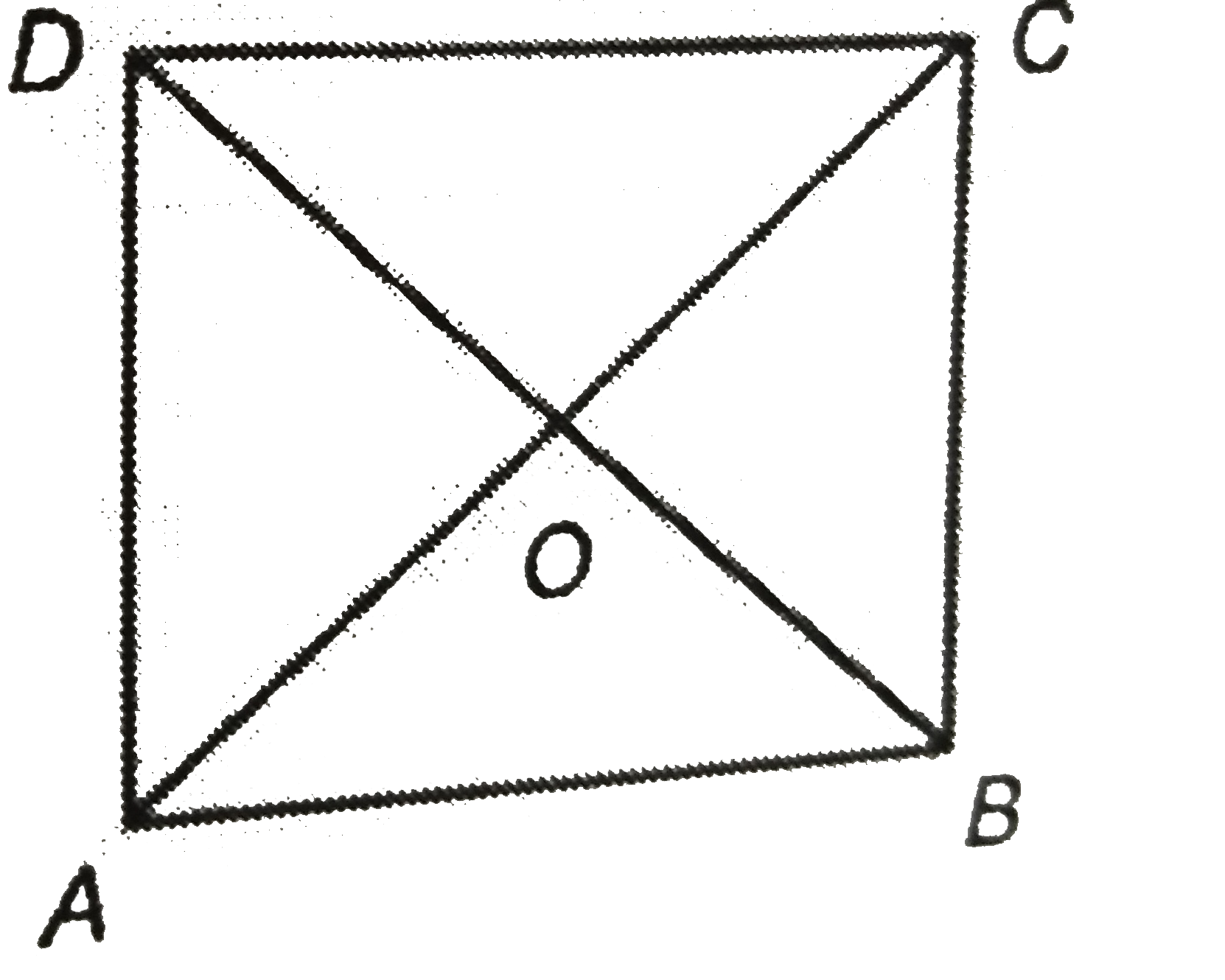
View SolutionThe co-ordinates of the vertex of a square ABCD are (1,2) and the equation of the diagonal BD is x+2y=10. Find the equation of other diagonal and the co-ordinates of the centre of the square.
View Solutionवर्ग ABCD का विकर्ण AC की लम्बाई 5.2 cm है। वर्ग का क्षेत्रफल ज्ञात करें?
View SolutionIf the end points of the diagonal of a square are (-2,3,1) and (-3,5,2) , then the length of the side of the square is
View SolutionIf (1, 2) and (3, 8) are a pair of opposite vertices of a square, find the equation of the sides and diagonals of the square.
View SolutionABCD एक वर्ग है । AB तथा AD को निर्देशाक्ष मानते हुए वर्ग के परिवर्तित का समीकरण ज्ञात कीजिए यदि मानते हुए वर्ग कि प्रत्येक भुजा कि लम्बाई l हो ।
View SolutionThe square of the diagonal of a square is 50 sq. units. Find the side of the square.
View SolutionThe sides of a square are .Find the equation of the circle drawn on the diagonal of the square as its diameter.
View SolutionThe sides of a square are .Find the equation of the circle drawn on the diagonal of the square as its diameter.
View SolutionThe side of a square are x = 1, x = 3, y = 2 and y = 4. Find the equation of the circle drawn on the diagonals of the square as its diameter
View Solution4 सेंमी भुजा वाले वर्ग का विकर्ण होगा-
View SolutionIf the length of diagonal BD of a square ABCD is 4.8 cm, the area of the square ABCD is :
View SolutionIf the length of diagonal BD of a square ABCD is 4.8 cm, the area of the square ABCD is :
View Solution