The Young’s modulus of three materials are in the ratio 2 : 2 : 1. Three wires made of these materials have their cross-sectional areas in the ratio 1 : 2 : 3. For a given stretching force the elongations in the three wires are in the ratioa 1 : 2 : 3b 3 : 2 : 1c 5 : 4 : 3d 6 : 3 : 4
Correct option d 6 : 3 : 4Explanation:l = FL/AY and for a given stretching force l ∝ 1/AYLet three wires have youngs modulus 2Y 2Y and Y and their cross sectional areas are A 2A and 3A respectively.
Related Solutions
The Young's modulus of three materials are in the ratio 2:2:1. Three wires made of these materials have their cross-sectional areas in the ratio 1:2:3. For a given stretching force the elongation's in the three wires are in the ratio
View SolutionThree wires of same material are connected in parallel to a source of emf. The length ratio of the wires is and the ratio of their area of cross section is then match the following
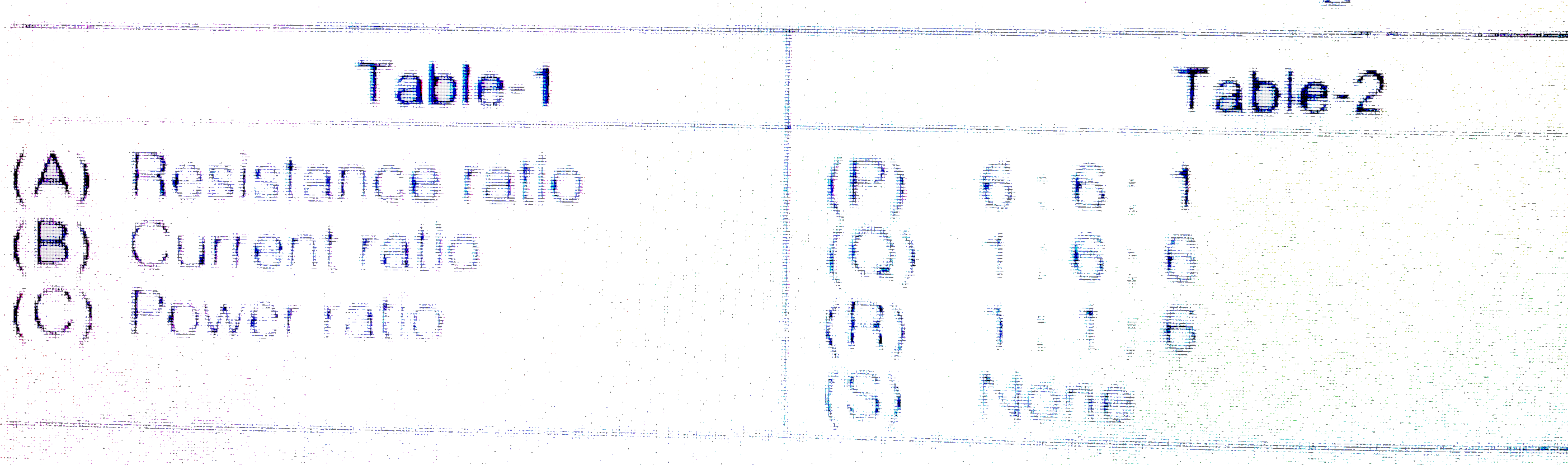
View SolutionThree wires of same material are connected in parallel to a source of emf. The length ratio of the wires is 1:2:3 and the ratio of their area of cross section is 2:4:1 then match the following
View Solutionतीन तारों के द्रव्यमानों का अनुपात और उनकी लम्बाइयों का अनुपात है। यदि तारें एक ही पदार्थ की बनी हों, तो उनके प्रतिरोधों का अनुपात होगा
View SolutionYoung modules of wire made of three different materials 2 : 2 : 1 . Proportion and the area of their cross section 1 : 2 : 3 Is proportional. The ratio of the increase in their length under the influence of the same tensile force.
View SolutionTwo pieces of wire, A and B of the same material have their lengths in the ratio 1:3 and their diameters are in the ratio 2:1 . If they are stretched by the same force, their elongations will be in the ratio
View SolutionTwo wires have diameters in the ratio , lengths in the ratio and Young's modulus in the ratio . The ratio of elongations produced in the wires when subjected to the same stretching force is
View SolutionTwo wires of same material , having cross-sectional areas in the ratio 1 : 2 and lengths in the ratio 1 : 4 are stretched by the same force. The ratio of the stresses in the wires will be ………….. .
View SolutionA 5 ampere current is distibuted in three branches. The ratio of the lengths of the wires in the three branches is 1:2:3.Determine the magnitude of current in each branch. The material and the cross sectional area of each wire are the same.
View SolutionTwo pieces of wire A and B of the same material have their lengths in the ratio 1 : 2 and their diameters in the ratio 2 : 1 if they are stretched by same force. Their elongation will be in the ratio of :
View SolutionTwo wires A and B of the same material have their length in the ratio 1:2 and diameters in the ratio 2:1.If they stretched by the same force the ratio of their elongation is
View SolutionIf a wire of length 4 m and cross-sectional area of is stretched by a force of 3 kN, then determine the change in length due to this force . Given, Young's modulus of material of wire is
View SolutionIf a wire of length 4 m and cross-sectional area of is stretched by a force of 3 kN, then determine the change in length due to this force . Given, Young's modulus of material of wire is
View Solutionतीन पदार्थों के यंग प्रत्यास्थता गुणांक 2:2:1 के अनुपात में है| इन पदार्थों से बने समान लम्बाई के तीन तारों के अनुप्रस्थ काटों के क्षेत्रफल के अनुपात में है| किसी दिए गए तनाव बल के लिए तारों की लम्बाई वृद्धियों में अनुपात ज्ञात कीजिए|
View SolutionTwo wires of same material , having cross-sectional areas in the ratio 1 : 2 and lengths in the ratio 1 : 4 are stretched by the same force. The ratio of the stresses in the wires will be ………….. .
View SolutionTwo wires of the same material but of lengths in the ratio 2:3 and diameters in the ratio of 3:2 are stretched with equal force. Then the ratio of elongations produced is
View SolutionTwo wires of same material of unchanged lengths in the ratio 2: 3 and diameters in the ratio 3 : 2 are stretched with equal forces . What is the ratio of their elongation produced ?
View SolutionTwo wires of different materials have resistances in the ratio 4 : 3 , lengths in the ratio 2 : 1 but have same radii of cross-section. Compare their resistivities.
View SolutionTwo wires of different materials having Young's moduli in the ratio lengths in the ratio and diameters in the ratio are stretched with the same force. The ratio of stress in the wires is
View SolutionTwo wires of different materials having Young's moduli in the ratio lengths in the ratio and diameters in the ratio are stretched with the same force. The ratio of stress in the wires is
View Solution