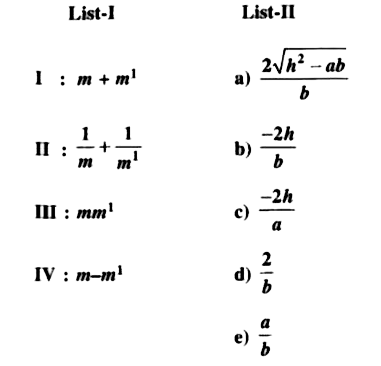
If h2 ≥ ab then the locus represented by the equation ax2 + 2hxy + by2 = 0 is a pair of lines passing through the origin.
Since a is real either a = 0 or a ≠ 0.Case 1: a = 0. In this case the given equation becomesy 2hx + by = 0 ...1 Since a = 0 at least one of the values of h and b is not zero so that 2hx + by = 0 is a first-degree equation and hence it represents a straight line. Also y = 0 represents x-axis. Hence Eq.1 represents pair of lines namely y = 0 i.e. x-axis and the line 2hx + by = 0. Case 2: a ≠ 0. In this case the equation is written as a2 x2 + 2ahxy + aby2 = 0ax + hy2 - h2 - aby2 = 0 ThereforeThe locus represented by the given equation is the pair of lines ax + h ± √h2 - ab y = 0 and both these lines pass through origin. When h2 = ab or h = b = 0 these two lines are identical coincide with each other.
Related Solutions
The equation
represents a pair of straight lines passing through the origin. The two lines are
View SolutionThe equation represents a pair of straight lines passing through the origin . The two lines are
View SolutionThe equation represents a pair of straight lines passing through the origin . The two lines are
View SolutionThe equation represents a pair of straight lines
passing through the origin. The two lines are
View SolutionThe equation represents a pair of straight lines passing through the origin . The two lines are
View SolutionThe equation represents a pair of straight lines passing through the origin . The two lines are
View SolutionThe equation represent a pair of st lines passing thro the origin the two lines are
View SolutionThe equation to the pair of lines through the origin which are perpendicular to the lines represented by is
View SolutionThe equation represented a pair of coincident lines through the origin if
View SolutionThe equation represents a pair of coincident lines through origin, if
View SolutionFind the equation of the pair of lines passing through the origin and perpendicular to the pair of lines
View SolutionFind the equation of the pair of lines passing through the origin and perpendicular to the pair of lines
View SolutionThe combined equation of the pair of lines through the origin and perpendicular to the pair of lines given by , is
View SolutionThe combined equation of the pair of lines through the origin and perpendicular to the pair of lines given by , is
View SolutionThe combined equation of the pair of lines through the origin and perpendicular to the pair of lines given by ax^(2)+2hxy+by^(2)=0 , is
View SolutionFind the equation of the pair of lines through the origin and perpendicular to the pair of line .
View SolutionThe equation represents a pair of perpendicular lines if
View SolutionIf the equation represents a pair of lines, then
View SolutionIf the equation represents two coincident straight lines passing through the origin , then h is equal to
View SolutionLet y = mx and be the lines represented by the equation ax2+2hxy+by+=0. Match the following and choose the correct answer.
View Solution