A point P moves on a square plate along a circular path radius r with a constant relative velocity vr. The plate moves horizontally with the constant acceleration a0 Fig.. Determine the magnitude of the absolute acceleration of P.
The components of the relative velocity in the moving reference frame ξ η are ∗: time derivative relative to the moving frame. Differentiation with respect to the moving frame leads to the components of the relative acceleration note:rφ∗=υr: Since the reference frame undergoes a translation the absolute acceleration is given by
Related Solutions
If a body moves along circular path of constant radius, then the magnitude of its acceleration will be
View SolutionA particle is moving along a circular path with a constant speed. the acceleration of the particle is constant
View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View SolutionA particles is moving on circular path of radius R with constant angular velocity omega . Its centripetal acceleration will be …... .
View SolutionAssertion : A particle moves along circular path with constant speed then acceleration must be present.
Reason : A particle moves with variable velocity then acceleration must be present.
View SolutionA particle is moving on a circular path with constant speed, then its acceleration will be constant in
View Solutionवृतीय पथ पर गति करते हुवे किसी पिंड के अभिकेंदर त्वरण का सूत्र कोणीय वेग और वृतीय पथ की त्रिज्या के पदों में लिहिये
View SolutionA particle starts moving with a constant angular acceleration in a circular path. The time at which the magnitudes of tangential and radial acceleration are equal is
View SolutionA particle starts moving with a constant angular acceleration in a circular path. The time at which the magnitudes of tangential and radial acceleration are equal is
View SolutionA particle starts moving with a constant angular acceleration in a circular path. The time at which the magnitudes of tangential and radial acceleration are equal is
View SolutionA body moving along a circular path of radius r with velocity V, has centripetal acceleration 'a'. If its velocity is made equal to 2V, then its centripetal acceleration is.
View SolutionA body moving along a circular path of radius R with velocity V , has centripetal acceleration a If its velocity is made equal to 2v , then its centripetal acceleration is
View SolutionA particle is moving along a circular path of radius 'r' with uniform angular velocity omega . Its angular acceleration is
View SolutionA particle is moving along an elliptical path with constant speed. As it moves from A to B, magnitude of its acceleration :
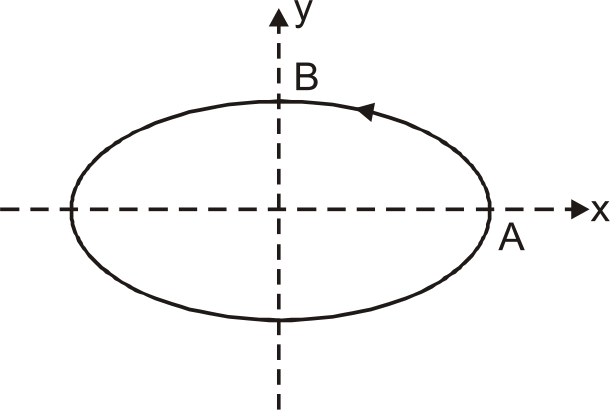
View SolutionA particle is moving along an elliptical path with a constant speed. As it moves from A to B, magnitude of its acceleration:
View SolutionA particle is moving along an elliptical path with constant speed. As it moves from A to B, magnitude of its acceleration :

View SolutionA particle of mass M moves in a circular path of radius r with a constant speed equal to V. Then its centripetal acceleration is
View SolutionA Particle of mass 'M' moves in a uniform circular path of radius 'r' with a constant speed 'v' then its centripetal acceleration is .
View SolutionA particle of mass M moves in a circular path of radius r with a constant speed equal to V. Then its centripetal acceleration is
View Solution