If a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them see figure de Broglie wavelength λdB of electrons can be calculated by the relationship n is an integerWave property of electrons implies that they will show diffraction effects. Davisson and Germer demonstrated this by diffracting electrons from crystals. The law governing the diffraction from a crystal is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructively see figure.a dcosi = nλdB b dsini = nλdBc 2dcosi = nλdB d 2dsini = nλdB.
c : Bragg’s relation nλ = 2dsinθ for having an intensity maximum for diffraction pattern.But as the angle of incidence is given nλ = 2dcosi is the formula for finding a peak.
Related Solutions
Wave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely
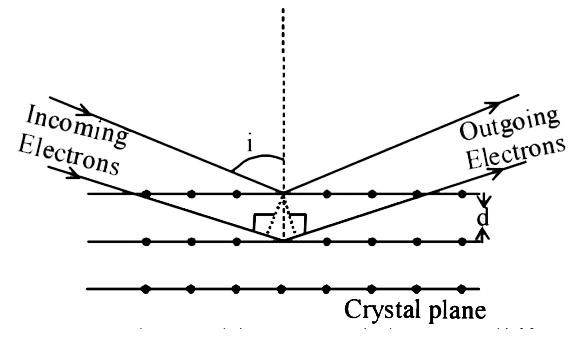
If a strong diffraction peak is observed when electrons are incident at an angle from the normal to the crystal planes with distance between them (see fig) de Brogle wavelength of electrons can be calculated by the relationship (n is an intenger)
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely

If a strong diffraction peak is observed when electrons are incident at an angle from the normal to the crystal planes with distance between them (see fig) de Brogle wavelength of electrons can be calculated by the relationship (n is an intenger)
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely If a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them (see fig) de Brogle wavelength lambda_(dB) of electrons can be calculated by the relationship (n is an intenger)
View SolutionDirection : Question Numbers. 150 and 151 are based on the following paragraph. Wave property of electrons implies that they will show diffraction effects. Davisson and Germer demonstrated this by diffracting electrons from crystals. The law governing the diffraction from a crystal is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructively (See figure). If a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them (see tigure), de-Broglie wavelength lamda_(dB) of electrons can be calculated by the relationship (n is an integer)
View SolutionThe wave properties of electrons indicate that they will exhibit diffraction effects. Davison and Germer explained this by the diffraction of electrons from the crystals. The rule governing diffraction from a crystal requires that the reflected electron waves from the plane of atoms in a crystal interfere (see Figure) If a strong diffraction peak is observed when electrons are incident at an 'i' angle from the rest of the crystal plane (see figure), the distance between them is 'd' then the de-Broglie wavelength of electrons lamda_(dB ) By what relation can it be calculated? (n is an integer)
View SolutionIf a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them (see figure), de-Broglie wavelength lamda_(dB) of electrons can be calculated by the relationship (n is an integer)
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructiely
Electron accelerated by potential are diffracted from a crystal if should be about
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructiely

Electron accelerated by potential are diffracted from a crystal if should be about
View SolutionThe wave property of electrons implies that they will exhibit diffraction effects. Davison and Zermer demonstrated this by diffraction of electrons from Christlow. The regulatory law of diffraction from a crystal is derived from the rich interference of the reflected electron waves from the plane of the atoms in the crystal. With the help of the above, choose the most appropriate answer to the following questions. If a strong diffraction peak is seen when the electrons are on the crystal bottom, between which the distance d is incident with the wavelength, then the de Broglie wavelength of the electrons is de Broglie. lambda _(dB) Can be deduced from this equation (n is an integer)
View SolutionWave property of electrons implies that they will show diffraction effects. Davission and Germer demonstrated this by diffracting electrons from crystals. The law governing the diffraction from a crystal is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructively (see figure) In an experiment, electrons are made to pass through a narrow slit of width 'd' comparable to either de-Broglie wavelength. They are detected on a screen at a distance 'D' from the slit The following graphs that can be expected to represent the number of electrons 'N' detected as a function of the detector position 'y' ( y=0 corresponds to the middle of the slit) is
View Solutionइलेक्ट्रॉन के तरंग गुण में यह अंतर्निहित है कि ये विवर्तन प्रभाव दर्शाएगें। डेवीसन तथा जर्मन ने इसे क्रिस्टलों द्वारा इलेक्ट्रॉनों को विवर्तित करके निर्देशित किया। क्रिस्टलों द्वारा इलेक्ट्रॉनों के विवर्तन की व्याख्या करने वाले नियम भी इस तथ्य पर आधारित है कि किसी क्रिस्टल में परमाणुओं के तलों से परिवर्तित इलेक्ट्रॉन तरंगों का संपोषी व्यक्तिकरण होता है आरेख दिखिए)।

जब दूरी के क्रिस्टल तलों (आरेख दिखिए) के अभिलंब से 'i' कोण पर इलेक्ट्रॉनों के आपतन से कोई प्रबल विवर्तन शिखर प्रकट होता है, तो इलेक्ट्रॉनों की डी - ब्रोग्ली तरंग दैर्ध्य के परिकलन के लिए उपयोग किया जाने वाला संबंध है (यहां n एक पूर्णांक है )
View SolutionDirection : Question Numbers. 150 and 151 are based on the following paragraph.
Wave property of electrons implies that they will show diffraction effects. Davisson and Germer demonstrated this by diffracting electrons from crystals. The law governing the diffraction from a crystal is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructively (See figure).
Electrons accelerate by potential V are diffracted from a crystal. If and , V should be about
View SolutionIn Davisson and Germer experiment, a crystal which diffracts a beam of electrons is of
View SolutionWave property of electrons implies that they will show diffraction effects. Davission and Germer demonstrated this by diffracting electrons from crystals. The law governing the diffraction from a crystal is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructively (see figure) The surface of a metal is illuminated with the light of 400 nm . The kinetic energy of the ejected photoelectrons was found to be 1.68 eV . The work function of the metal is : ( hc = 1240 eV-nm )
View SolutionWave property of electrons implies that they will show diffraction effects. Davission and Germer demonstrated this by diffracting electrons from crystals. The law governing the diffraction from a crystal is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructively (see figure) The surface of a metal is illuminated with the light of 400 nm . The kinetic energy of the ejected photoelectrons was found to be 1.68 eV . The work function of the metal is : ( hc = 1240 eV-nm )
View SolutionWave property of electrons implies that they will show diffraction effects. Davission and Germer demonstrated this by diffracting electrons from crystals. The law governing the diffraction from a crystal is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructively (see figure) The surface of a metal is illuminated with the light of 400 nm . The kinetic energy of the ejected photoelectrons was found to be 1.68 eV . The work function of the metal is : ( hc = 1240 eV-nm )
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely Electron accelerated by potential V are diffracted from a crystal if d = 1 Å and i = 30^(@), V should be about (h = 6.6 xx 10^(-34) Js, m_(e) = 9.1 xx 10^(-31) kg , e = 1.6 xx 10^(-19)C)
View SolutionThe wave properties of electrons indicate that they will exhibit diffraction effects. Davison and Germer explained this by the diffraction of electrons from the crystals. The rule governing diffraction from a crystal requires that the reflected electron waves from the plane of atoms in a crystal interfere (see Figure) Electrons accelerated by potential V are reversed from a crystal. If d= 1A And i=30^@ Is V should be approx. (h=6.6 xx 10^(-34)Js, m_e -9.1 xx 10^(-31) kge=1.6 xx 10^(-19) C)
View SolutionThe wave properties of electrons indicate that they will exhibit diffraction effects. Davison and Germer explained this by the diffraction of electrons from the crystals. The rule governing diffraction from a crystal requires that the reflected electron waves from the plane of atoms in a crystal interfere (see Figure) In one experiment, electrons are passed through a narrow slit of width 'd' equal to their given Broglie wavelength. They are communicated on a screen at a distance 'D' from the slit. (View pictures) Which of the following diagrams can represent the number of electrons detected 'N' as a function of the position 'y' of the detector? (y = 0 corresponds to the middle of the slit)
View SolutionIn the Davisson-Germer experiment if the incident beam consists of electrons, then the diffracted beam consists of :
View Solution