The distance of the line ax + by + c = 0 from the point Px1 y1 is |ax1 + by1 + c|/√ax1 + by1 + c/√a2 + b2
See Fig. Shift the origin to the point Px1 y1 and let the new coordinates of any point be denoted by X Y. Hence we have x = X + x1 and y = Y + y1 so that P becomes 0 0 and the equation of the given line is aX + x1 + bY + y1 + c = 0. That is aX + bY + ax1 + by1 + c = 0 2.5Hence the distance of the line [Eq. 1] from P0 0 is equal to
Related Solutions
If the mean of n observations ax1, ax2, ax3, ...., axn is aX show that (ax1-aX) + (ax2-aX) + .....+ (axn - aX) = 0
View SolutionIf the mean of n observations ax1, ax2, ax3, ...., axn is aX show that (ax1-aX) + (ax2-aX) + .....+ (axn - aX) = 0
View SolutionProve that the incentre of the triangle whose vertices are given by A(x1,y1),B(x2,y2),C(x3,y3)is(ax1+bx2+cx3)/(a+b+c),(ay1+by2+cy2)/(a+b+c) where a b,and c are the sides opposite to the angles A,B and C respectively.
View SolutionIf the equation of the locus of a point equidistant from the points (a_1, b_1) and (a_2, b_2) is (a_1-a_2)x+(b_1-b_2)y+c=0 , then the value of c is a a2-a2 2+b1 2-b2 2 sqrt(a1 2+b1 2-a2 2-b2 2) 1/2(a1 2+a2 2+b1 2+b2 2) 1/2(a2 2+b2 2-a1 2-b1 2)
View SolutionIf the equation of the locus of a point equidistant from the points and is , then the value of is
View SolutionIf c is negative then the distance of the straight line from the origin is -
View SolutionIf the angles A,B,C of a triangle are in A.P.and sides a,b,c are in G.P. ,then a2,b2,c2 are in
View SolutionFor a> b>c>0 , if the distance between (1,1) and the point of intersection of the line ax+by-c=0 is less than 2sqrt2 then,
View SolutionFor , the distance between (1, 1) and the point of intersection of the lines ax+by+c =0 and bx+ay+c=0 is les than . Then
View SolutionThe area of the figure formed by the lines and is
View SolutionThe perpendicular distance from origin to the line ax+by+c=0 is
View Solutionरेखाओं और द्वारा बनी आकृति का क्षेत्रफल क्या है?
View SolutionIf a,b,c are in A.P then the lines represented by ax+by+c=0 are concurrent at the point
View SolutionOMR|Different Forms Of Ax+By+C=0|Questions|Distance Of A Point From A Line|Questions|Distance Between Two Parallel Lines|Questions
View SolutionThe equation of the straight line, which has the same inclination from the axes and the distance from the points (1, -2) and (3, 4) is ax + by + c = 0, where
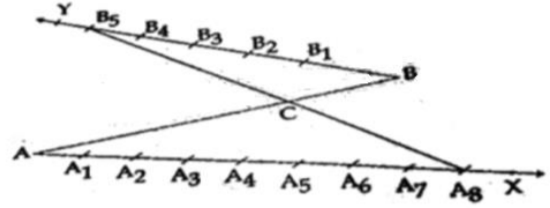
View SolutionIn the figure, if B1, B2, B3,…... and A1,A2, A3,….. have been marked at equal distances. In what ratio C divides AB?
View SolutionIf the line ax +by +c=0 passes through the fixed point which is
View SolutionIf |(a,b-c,b+c),(a+c,b,c-a),(a-b,a+b,c)|=0 then the line ax+by+c=0 passes through the fixed point which is
View SolutionIf |(a,b-c,b+c),(a+c,b,c-a),(a-b,a+b,c)|=0 then the line ax+by+c=0 passes through the fixed point which is
View SolutionIf a, c, b are in G.P then the line
View Solution