Two first-degree equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 represent parallel lines if and only if a1b2 = a2b1 i.e. a1:b1 = a2:b1i.e a1:b1 = a2 : b2.
When two lines are parallel both are either vertical or non-vertical. If both are vertical then b1 = b2 = 0 so that a1b2 = a2b1 = 0. If both are non-vertical their slopes are equal.Thus - a1/b1 = -a2/b2Hence a1b2 = a2b1 or a1:b1 = a2:b2 Conversely when a1b2 = a2b1 and if b1 = 0 then a1 ≠ 0 so that b2 = 0. Therefore b1 = 0 ⇔ b2 = 0 and hence if one of the lines is vertical then the other is also vertical so that the given lines are parallel. If both b1 and b2 are non-zero then Since the slopes are equal the lines are parallel.
Related Solutions
সংখ্যারেখা তৈরি করে নীচের সংখ্যাগুলিকে সংখ্যারেখায় দেখাও ও নাম দাও। +5, -2, +3, -6, +2, -5, -এ যথাক্রমে A,B,C,D,E ও F নাম দাও। B থেকে E-এর দূরত্ব কত ঘর মেপে দেখো।
View SolutionIf the equation of the locus of a point equidistant from the points (a_1, b_1) and (a_2, b_2) is (a_1-a_2)x+(b_1-b_2)y+c=0 , then the value of c is a a2-a2 2+b1 2-b2 2 sqrt(a1 2+b1 2-a2 2-b2 2) 1/2(a1 2+a2 2+b1 2+b2 2) 1/2(a2 2+b2 2-a1 2-b1 2)
View SolutionIf the equation of the locus of a point equidistant from the points and is , then the value of is
View SolutionA(a1, b1) மற்றும் B(a2, b2) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத் துண்டை X-அச்சு எந்த விகிதத்தில் பிரிக்கும்?
View SolutionThe ratios a1/a2 , b1/b2 , c1/c2 Find out whether the given linear equations are pairwise compatible or incompatible: 2x - 3y = 8 and 4x - 6y = 9.
View SolutionIf (1+x-3x^(2))^(2145)=a0+a1x+a2x^(2)+... then a0-a1+a2-a3+...... ends with
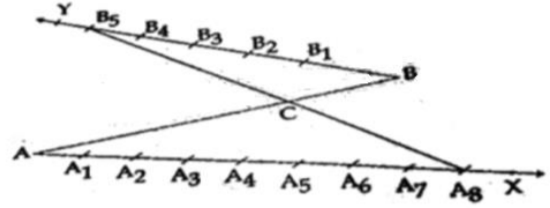
View SolutionIn the figure, if B1, B2, B3,…... and A1,A2, A3,….. have been marked at equal distances. In what ratio C divides AB?
View SolutionSuppose A1,A2,…..A30 are thirty sets each having 5 elements and B1,B2,…….Bn are n sets each having 3 elements.Let each elements of S belongs to exactly 10 of A1,'s and exactly 9 of B1's.Then find the value of n.
View SolutionIn a , If , then is
View SolutionIf and be the first, second and third ionization constant of and . Then which is/are correct ?
View SolutionIf x,y,z are in A.P.and A1 is the arithmetic mean of x,y and A2 is the arithmetic mean of y,z then prove that the arithmetic mean of A1 and A2 isy
View SolutionThe activation energies of two raction are and with . If the temperature of the reacting systems is increased from to predict which of the following alternatives is correct
View SolutionThe activation energies of two reactions are and with . If the temperature of the reacting systems is increased from to , which of the following is correct?
View SolutionThe activation energies of two reactions are E_(a1) and E_(a2) with E_(a1) gt E_(a2) . If the temperature of the reacting systems is increased from T_(1) to T_(2) predict which of the following alternatives is correct
View SolutionThe activation energies of two reactions are E_(a1) and E_(a2) with E_(a1) gt E_(a2) . If the temperature of the reacting systems is increased from T to T' , which of the following is correct?
View SolutionA reactant (A) forms two products : A overset (k_1) rarr B , Activation energy, E_(a1) Aoverset (k_2) rarr C , Activation energy, E_(a2) If E_(a2) = 2E_(a1) , then k_1 and k_2 are related as
View SolutionThe activation energies of two reactions are E_(a1) and E_(a2) with E_(a1) gt E_(a2) . If the temperature of the reacting systems is increased from T to T' , which of the following is correct?
View SolutionIf are arithmetic means inserted between the numbers a and b, then find the value of
View Solutionजल में के लिए क्यों है?
View SolutionThe domain of f(x)=log_(a1)log_(a2)log_(a3)log_(a4)(x)(a_(i)>0) is
View Solution