The mass density of a certain planet has spherical symmetry but varies in such a way that the mass inside every spherical surface with center at the center of the planet is proportional to the radius of the surface. If r is the distance from the center of the planet to a point mass inside the planet the gravitational force on the mass is: A. not dependent on r B. proportional to r2 C. proportional to r D. proportional to 1/r E. proportional to 1/r2
D. proportional to 1/r
Related Solutions
A spherical hypothesized planet of mass M and radius R is composed entirely of incompressible liquid. If the pressure on the surface of the planet is zero, then the pressure at the center of the planet is [G=universal gravitational constant]
View SolutionA spherical hypothesized planet of mass M and radius R is composed entirely of incompressible liquid. If the pressure at the surface of the planet is zero, then the pressure at the center of the planet is: [G = Universal gravitational constant]
View Solutionएक बहुत कम द्रव्यमान वाली छोटी वस्तु को एक वेग से इस प्रकार फेंका गया है कि (3M द्रव्यमान एवं 2R त्रिज्या) ग्रह से (M द्रव्यमान एवं R त्रिज्या) वाले दूसरे ग्रह तक पहुँच सके। दोनों ग्रहों के केन्द्र से केन्द्र से बीच की दूरी 6R है, वस्तु की बड़े ग्रह के केन्द्र से दूरी इस क्षण 'x' है। यात्रा के दौरान वह दूरी x ज्ञात कीजिए जहाँ वस्तु की चाल (a) अधिकतम (b) न्यूनतम होगी। मान लीजिए कि वस्तु ग्रहों के केन्द्रो को मिलाने वाली रेखा पर ही गतिमान है।
View Solutionஒரு கோளின் புவிஈர்ப்பு முடுக்கம், புவியின் பரப்பின் மீதான ஈர்ப்பு முடுக்கத்தில் பாதி மற்றும் கோளின் ஆரம் புவியின் ஆரத்தில் பாதி, கோளின் நிறையை புவியின் நிறையில் கண்டுபிடி.
View SolutionEscape velocity of a body from the surface of a spherical planet of mass M, radius R and density p is
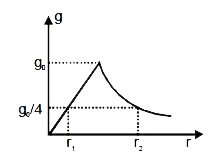
View Solutionचित्र में एक समान गोलीय ग्रह के केन्द्र से दूरी के साथ गुरूत्वीय त्वरण का परिवर्तन दर्शाया गया है। ग्रह की त्रिज्या R है। होगा :
View SolutionThe ratio of the weight of a body on the Earth’s surface to that on the surface of a planet is 9 : 4. The mass of the planet is of that of the Earth. If ‘R’ is the radius of the Earth, then the radius of the planet is where n is ___________ . (Take the planets to have the same mass density)
View SolutionThe ratio of the weight of a body on the Earth’s surface to that on the surface of a planet is 9 : 4. The mass of the planet is 1/9 of that of the Earth. If ‘R’ is the radius of the Earth, then the radius of the planet is where n is ___________ . (Take the planets to have the same mass density)
View SolutionWhat will be the gravitational potential on the surface of a planet of mass M and radius R ?
View Solutionसुदूर अंतरिक्ष में स्थित एक गोलाकार ग्रह का द्रव्यमान M तथा व्यास d में है । m द्रव्यमान का एक कण इस ग्रह की सतह के निकट से स्वतंत्रतापूर्वक गिर रहा है । इस कण का गुरुत्वीय त्वरण अनुक्रमानुपाती होगा-
View SolutionThe spherical planets have the same mass but densities in the ratio . For these planets the :
View Solutionगोलाकार ग्रहों के द्रव्यमान समान है, लेकिन घनत्व 1:8 के अनुपात में है। इन ग्रहों के लिए :
View SolutionThe spherical planets have the same mass but densities in the ratio 1: 8 . For these planets the :
View SolutionA point mass m is placed inside the spherical shell of radius R and mass m. The gravitational force exerted by the shell at a point mass at R / 2 distance from the center of the shell is
View Solutionद्रव्यमान M और त्रिज्या R के एक ठोस गोले में, त्रिज्या की एक गोलीय गुहिका इस प्रकार बनाई गई है कि गुहिका का केंद्र गोले के केंद्र से से दूरी पर है। एक बिंदु द्रव्यमान m को गोले के केंद्र से की दूरी पर गुहिका के अंदर रखा जाता है। गोले और बिंदु द्रव्यमान m के बीच गुरुत्वाकर्षण खिंचाव है
View SolutionThe forces of two spherical planets are equal but their density is 1: 8, so the ratio of the gravitational acceleration on the surface of the planets for these two planets is ..........
View SolutionAssertion : If the projuct of surface area and density is same for both Reason : Product of surface area and density is proportional to the mass of the planet per unit radius f the planet.
View SolutionThe masses of two spherical planets A and B are M_(A) and M_(B) , surface areas are S and 9 S respectively. The mass of a spherical planet C is (M_(A) + M_(B)) . If the densities of all the planets A, B, C are same, then the escape velocities V_(A) , V_(B) , V_(C) from the surface of these planets follow:
View SolutionTwo spherical planets P and Q have the same uniform density rho masses M_p and M_q and surface areas A and 4A respectively A spherical planet R also has uniform density rho and its mass is (M_p+M_q) the escape velocities from the planets P,Q and R are V_p,V_Q,V_R respectively then
View SolutionTwo spherical planets P and the same densities have masses respectively. M_P And M_Q And the surface area is A and 4A, a spherical planet R also has the same density. rho and its mass (M_P+M_Q) The escape velocities from the planets P, Q and R are respectively v_pv_Q And v_R is then
View Solution