The force acting on a particle of mass m moving along the x-axis is given by Fx = Ax2 − Bx. Which one of the following is the potential energy of the particle? A. 2Ax - BB. - x2/62Ax - 3D C. Ax3 - Bx2 D. Zero
Correct option b —x2/6 2Ax — 3BExplanation:Potential Energy = - ∫ Fx dx Ux = - ∫ Ax2 - Bx dx Ux = - Ax3/3 + Bx2/2 Ux = -x2/6 2Ax - 3B.
Related Solutions
The force acting on a particle of mass m moving along the x-axis is given by F (x) = Ax^(2) - Bx. Which one of the following is the potential energy of the particle?
View Solutionx- अक्ष के समानान्तर गतिमान m द्रव्यमान वाले एक कण पर कार्यकारी बल को द्वारा निरूपित किया गया है । इस कण की स्थितिज ऊर्जा निम्नलिखित में से कौन -सी है ?
View SolutionIn figure, the variation of potential energy of a particle of mass is represented w.r.t its x-coordinate. The particle moves under the effect of the conservative force along the x-axis. Which of the following statements is incorrect about the particle?
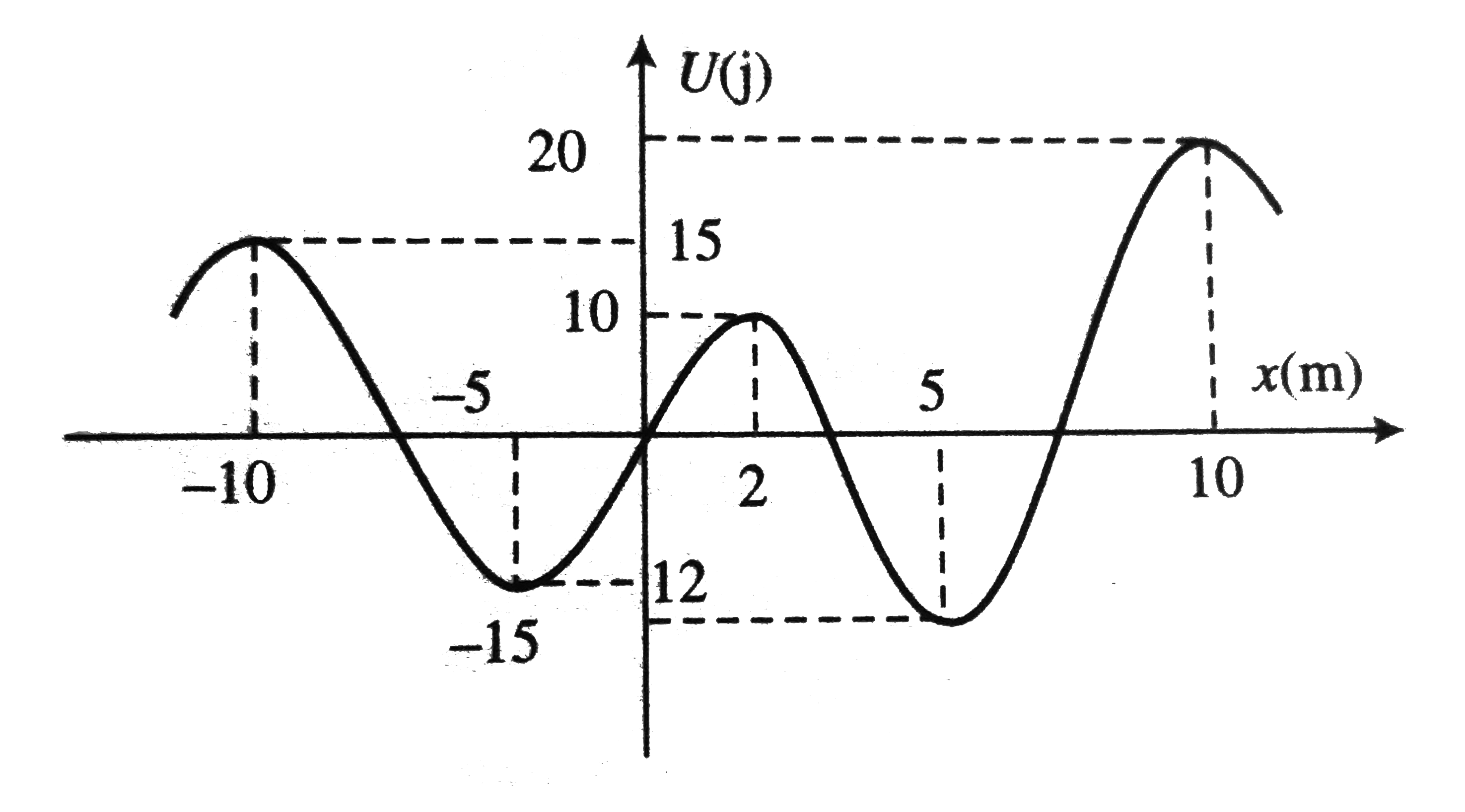
View SolutionIn figure, the variation of potential energy of a particle of mass m=2kg is represented w.r.t its x-coordinate. The particle moves under the effect of the conservative force along the x-axis. Which of the following statements is incorrect about the particle?
View SolutionIn the figure the variation of potential energy of a particle of mass m=2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis. Which of the following statements are correct about the particle:
View SolutionThe potential energy U(x) of a particle moving along x - axis is given by . Find the equilibrium position of particle.
View SolutionThe potential energy U(x) of a particle moving along x - axis is given by U(x)=ax-bx^(2) . Find the equilibrium position of particle.
View SolutionA particle moves along the X - axis with velocity . What will be work done by the forces acting on particle during interval it moves from x = 0 to x = d ? (Assume mass of the aprticle is m ) .
View SolutionA force F = alpha +beta x acts on a particle of mass m along the X . Axis . Here alpha and beta are constants . Find the work done by this force when particle moves form x = 0 to x = d .
View SolutionIn the figure, the variation of potential energy of a particle of mass m = 2kg is represented with respect to its x-coordinate. The particle moves under the effect of this conservative force along the X-axis.
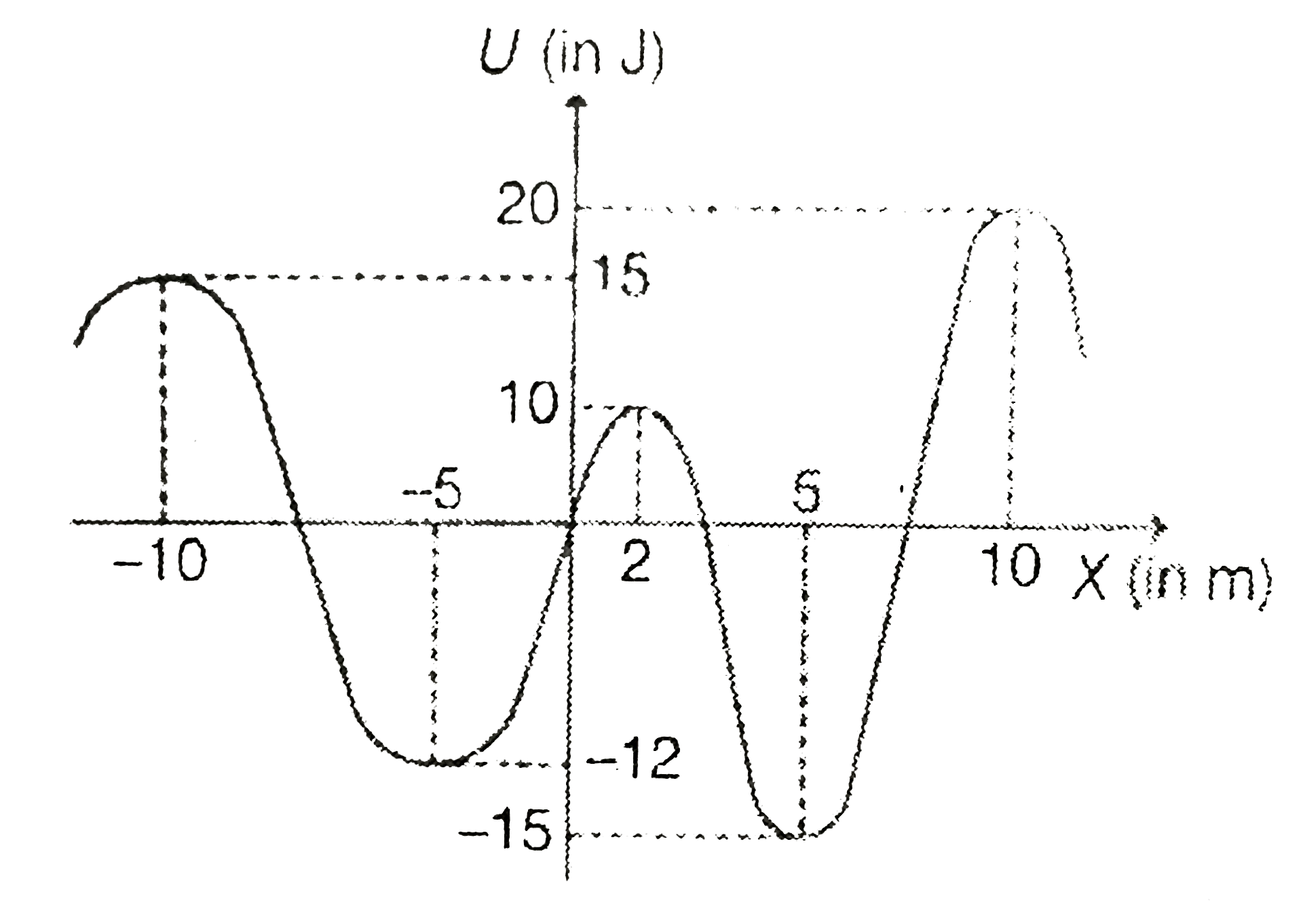
If the particle is released at the origin, then
View SolutionIn the figure the variation of potential energy of a particle of mass is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis.
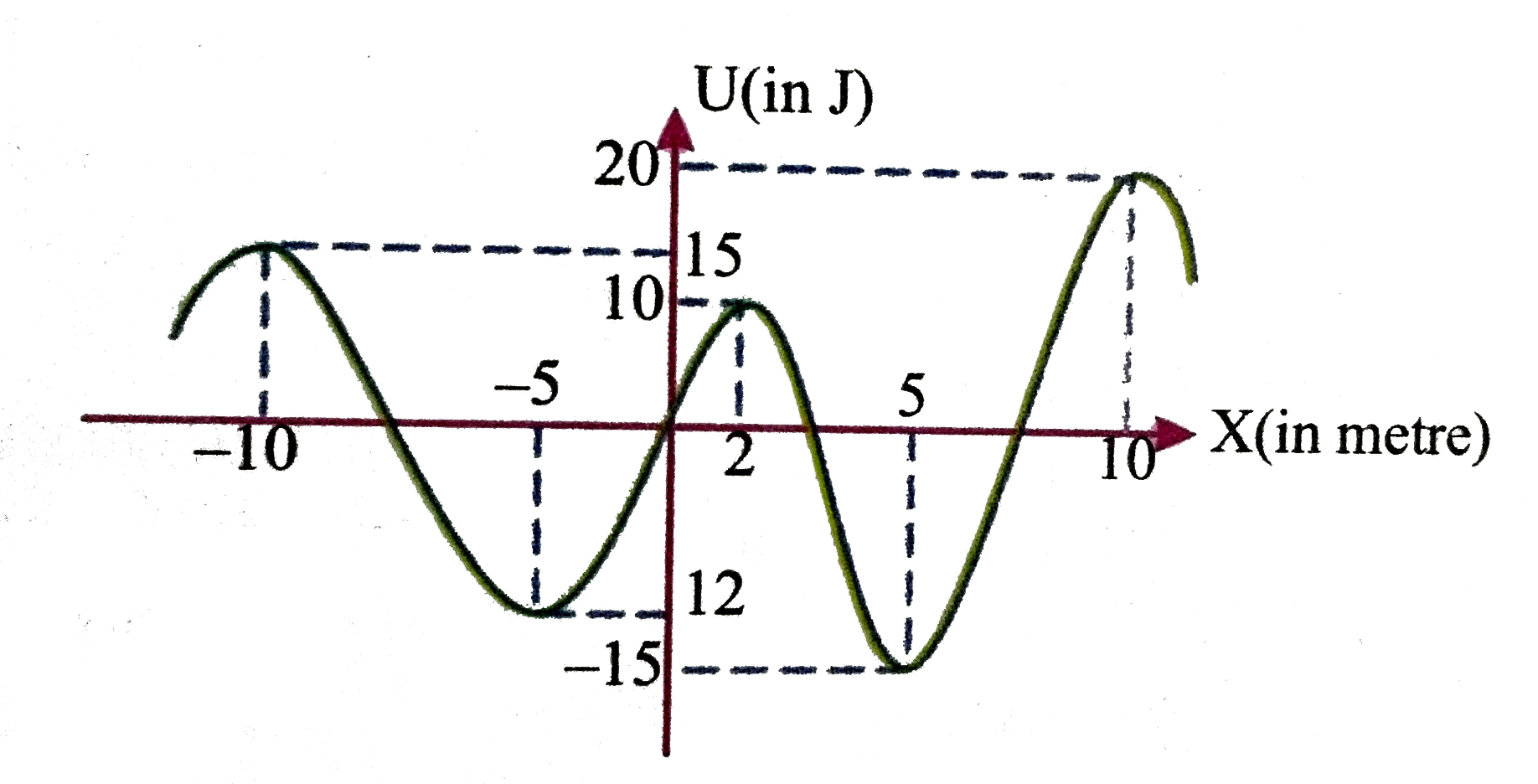
If the particle is released at the origin then
View SolutionThe potential energy of a particle of mass 1 kg moving along x-axis given by U(x)=[(x^(2))/(2)-x]J . If total mechanical energy of the particle is 2J then find the maximum speed of the particle. (Assuming only conservative force acts on particle)
View SolutionThe potential energy of a particle of mass 1 kg free to move along x-axis is given by U(x) =(x^(2)/2-x) joule. If total mechanical energy of the particle is 2J then find the maximum speed of the particle. (Assuming only conservative force acts on particle)
View Solutionm द्रव्यमान का एक कण नियत बल के अंतर्गत X - अक्ष के अनुदिश गतिशील है। कण के वेग तथा स्थिति के समीकरण व्यत्पन्न करो।
View SolutionThe rate of doing work by force acting on a particle moving along x-axis depends on position x of particle and is equal to 2x. The velocity of particle is given by expression :-
View SolutionThe rate of doing work by force acting on a particle moving along x-axis depends on position x of particle and is equal to 2x. The velocity of particle is given by expression :-
View SolutionThe rate of doing work by force acting on a particle moving along x-axis depends on position x of particle and is equal to 2x. The velocity of particle is given by expression :-
View SolutionA single conservative fore F_(x) acts on a 2kg particle that moves along the x-axis. The potential energy is given by. U =(x-4)^(2)-16 Here, x is in metre and U in joule. At x =6.0 m kinetic energy of particle is 8 J find . (a) total mechanical energy (b) maximum kinetic energy (c) values of x between which particle moves (d) the equation of F_(x) as a funcation is zero (e) the value of x at which F_(x) is zero .
View SolutionA single conservative fore F_(x) acts on a 2kg particle that moves along the x-axis. The potential energy is given by. U =(x-4)^(2)-16 Here, x is in metre and U in joule. At x =6.0 m kinetic energy of particle is 8 J find . (a) total mechanical energy (b) maximum kinetic energy (c) values of x between which particle moves (d) the equation of F_(x) as a funcation is zero (e) the value of x at which F_(x) is zero .
View SolutionA particle of mass m is free to move along x axis under the influence of a conservative force. The potential energy of the particle is given by U=-ax^(x) e^(-bx) [a and b are positive constants] Find the frequency of small oscillations of the particle about its equilibrium position
View Solution