The system in Fig.consists of three bars and a beam with negligible masses and a block mass m. Determine the circular frequency of the free vertical vibrations.
The system consisting of the truss and the beam is equivalent to a system consisting of two springs in parallel both springs undergo the same elongation when the block is displaced. To determine the spring constant kB of the beam we subject the beam to the force FB = 1 which acts at the location of the block. This force produces the deflectionThus the spring constant is given byIn order to find the spring constant kT of the truss we apply the force FT = 1 at bar ①. This force causes the displacementWithwe obtainNow we replace the two springs in parallel by an equivalent single spring. Its spring constant k∗ is given byThus the eigenfrequency is
Related Solutions
एक प्रयोग में एक डोरी n खण्डों में कम्पन कर रही है, जबकि M द्रव्यमान का पिण्ड एक कढ़ाई में रखा है। कढ़ाई मे कितना द्रव्यमान रखा जाये ताकि वह 2n खण्डों मे समान आवृत्ति से कम्पन करे? कढ़ाई का द्रव्यमान नगण्य है।
View SolutionA mass m is vertically suspended from a spring of negligible mass, the system oscillates with a frequency n. what will be the frequency of the system, if a mass is suspended from the same spring?
View SolutionA mass m is vertically suspended from a spring of negligible mass, the system oscillates with a frequency n. what will be the frequency of the system, if a mass 4m is suspended from the same spring?
View SolutionA mass m is vertically suspended from a spring of negligible mass, the system oscillates with a frequency n. What will be the frequency of the system, if a mass 4m is suspended from the same spring?
View SolutionA block of mass M is attached to the lower end of a vertical rope of mass m. An upward force P acts on the upper end of the rope. The system is free to move. The force exerted by the rope on the block is
View SolutionThe time period for small vertical oscillations of block of mass m when the masses of the pulleys are negligible and spring constant and is
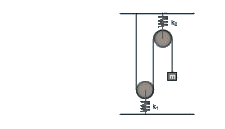
View SolutionThe frequency of vertical oscillations of the three spring-mass system, shown in figure, is
View Solution(A): A undamped springp-mass system is simplest free vibration system.
(R): It has three degrees of freedom.
View SolutionFigure shows three systems in which a block of mass m can execute S.H.M. What is ratio of frequency of oscillation?
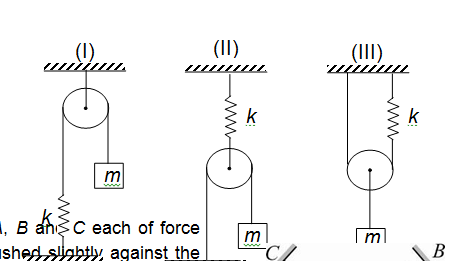
View SolutionFigure shows three systems in which a block of mass m can execute S.H.M. What is ratio of frequency of oscillation?

View SolutionA block of mass M is attached to the lower end of a vertical rope of mass m. An upward force Pacts on the upper end of the rope. The system is free to move. The force exerted by the rope on the block is
View SolutionTwo beads of mass 2m and m , connected by a rod of length l and of negligible mass are free to move in a smooth vertical circular wire frame of radius l as shown. Initially the system is held in horizontal position ( Refer figure ) The minimum velocity that should be given to the mass 2m in clockwise direction to make it vertical is :
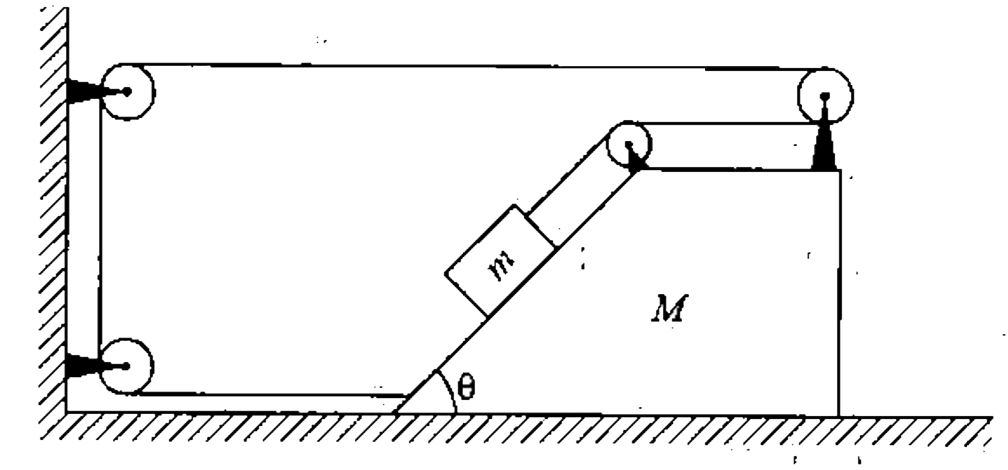
View SolutionFigure-2.64 shows a block of mass M supporting a bar of mass m through a pulley system. If system is released from rest, find the acceleration of block M and the tension in the strings
View SolutionA block of mass m slides down a smooth vertical circular track. During the motion, the block is in
View SolutionA block of mass m slides down a smooth vertical circular track. During the motion, the block is in:
View SolutionA block of mass m slides down a smooth vertical circular track. During the motion, the block is in
View SolutionA block of mass m slides down a smooth vertical circular track. During the motion, the block is in
View SolutionThree blocks A,B, and C are suspended as shown in fig. Mass of each of blocks A and B is m. If the system is in equilibrium, and mass of C is M then

View SolutionThree blocks A,B and C are suspended as shown in the figure. Mass of each block A and C is m. if the system is in equilibrium and mass of B is M, then

View SolutionThree blocks A,B, and C are suspended as shown in fig. Mass of each of blocks A and B is m. If the system is in equilibrium, and mass of C is M then

View Solution