The angled member weight W = mg in Fig. consists of two homogeneous bars. Derive the equation of motion for the member’s center of mass.
First we locate the center of mass of the angled member. With the coordinate system as shown in the figure we obtainThus the distance of the center of mass from point A is given byThe member rotates about a fixed axis that passes through A. We introduce the angle ϕ and apply the principle of angular momentum:ΘA ϕ¨ =MAWe measure ϕ from the position of equilibrium C is vertically below A. With the mass moment of inertiawe obtainNote: In the case of small oscillations ϕ ≪ 1 sinϕ ≈ ϕ the equation of motion reduces to the differential equationfor harmonic vibrations.
Related Solutions
A bar of W weight is placed on two parallel sharp points A and B and the bar is horizontal. The distance between the two sharp points is d. The center of gravity of the bar is located at a distance of x from A. The perpendicular reaction to A is.
View SolutionA drum major's baton consists of two masses m_(1) and m_(2) separated by a thin rod length l. The baton is thrown into the air. The problem is to find the baton's center of mass and the equation of motion for the center of mass.
View SolutionA drum major's baton consists of two masses m_(1) and m_(2) separated by a thin rod length l. The baton is thrown into the air. The problem is to find the baton's center of mass and the equation of motion for the center of mass.
View SolutionA drum major's baton consists of two masses m_(1) and m_(2) separated by a thin rod length l. The baton is thrown into the air. The problem is to find the baton's center of mass and the equation of motion for the center of mass.
View SolutionDerive an expression for the center of mass of two point masses.
View SolutionFind the value of x in the following figures.
View SolutionA non-uniform bar of weight 'w' is suspended at rest by two strings of negligible weight. The angles made by the strings with the vertical are 36.9^(@) and 53.1^(@)C respectively. The bar is 2m long. Calculate the distance 'd' of the centre of gravity of the bar from its left. (refer fig).-NCERT
View SolutionA non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Fig.7.39. The angles made by the strings with the vertical are and respectively. The bar is 2 m long. Calculate the distance d of the centre of gravity of the bar from its left end.
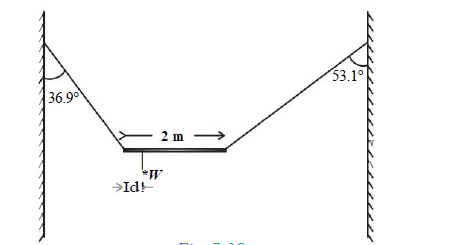
View SolutionA non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Fig. The angles made by the strings with the vertical are 36.9^(@) and 53.1^(@) respectively. The bar is 2m long. Calculate the distance d of the centre of gravity of the bar from its left end.
View SolutionA non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Fig. The angles made by the strings with the vertical are 36.9^(@) and 53.1^(@) respectively. The bar is 2m long. Calculate the distance d of the centre of gravity of the bar from its left end.
View SolutionA non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Fig.7.39. The angles made by the strings with the vertical are 36.9^(@) and 53.1° respectively. The bar is 2 m long. Calculate the distance d of the centre of gravity of the bar from its left end.
View SolutionA non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Fig.7.39. The angles made by the strings with the vertical are 36.9^@ and 53.1^@ respectively. The bar is 2 m long. Calculate the distance d of the centre of gravity of the bar from its left end.
View SolutionThe motion of the center of mass of a system consists of many particles describes its
View SolutionThe average molecular weight of the synthesized polymers, bar(M_n) And weighted atomic mass barM_(w) Is related to
View Solutionसमजातीय श्रेणी के दो क्रमागत सदस्यों में किस समूह का अन्तर होता है?
View SolutionFind two unit vectors each of which makes equal angle with bar(u), bar(v) and bar(w) .
View SolutionDerive an expression for motional emf in a rotating bar.
View SolutionGraphical Derivation OF Equation OF Motion || Newton Equation OF Motion
View SolutionThe motion of center of mass depends on
View SolutionTwo homogeneous spheres A and B of masses m and 2m having radii 2a and a respectively are placed in contact. The distance of the center of mass of the body from the center of the sphere A is:
View Solution