A homogeneous beam mass m length l rotates about frictionless support A Fig. until it hits support B. The motion starts with zero initial velocity in the vertical position. The coefficient of restitution e is given. Calculate the impulsive forces at A and B. Determine the distance a so that the impulsive force at A vanishes. Calculate the change of the kinetic energy.
First we calculate the angular velocity of the beam immediately before the impact with the aid of the conservation of energy ΘA = ml2/3:We then apply the principles of impulse and momentum:Here the velocity of the center of mass and the angular velocity before the impact are given byIn order to obtain the velocities immediately after the impact we use the hypothesiswhich leads toSolving for the impulsive reactions yieldsThe impulsive force at A vanishes ifThe change of the kinetic energy is the difference ∆T = T1 − T0 of the energies before and after impact:
Related Solutions
A uniform beam of length . And mass is supported as shown. Of the cable suddenly breaks, determine ,
(a) the acceleration of end .
(b) the reaction at the pin support.
 .
.
View SolutionA uniform beam of length L . And mass m is supported as shown. Of the cable suddenly breaks, determine , (a) the acceleration of end B . (b) the reaction at the pin support. .
View SolutionA force of 5 N acts on a body for 2 milliseconds. Calculate the impulse. If the mass of the body is 5 g, calculate the change of velocity.
View SolutionA force of 5 N acts on a body for 2 milliseconds. Calculate the impulse. If the mass of the body is 5 g, calculate the change of velocity.
View SolutionA force of 5 N acts on a body for 2 milliseconds. Calculate the impulse. If the mass of the body is 5 g, calculate the change of velocity.
View SolutionA force of 5 N acts on a body for 2 milliseconds. Calculate the impulse. If the mass of the body is 5g, calculate the change of velocity.
View SolutionImpulsive and Non Impulsive Force|| Impulse Momentum Theorem || Calculation OF Impulse
View Solution10N force on an object 3mus (microseconds). If the mass of the object is 5gm, calculate the change in impulse and velocity.
View SolutionHow will you calculate the length of the S period.
View SolutionImpulse due to a Force | Collisions: basics, coefficient of restitution | Head-on collisions
View SolutionImpulse due to a Force | Collisions: basics, coefficient of restitution | Head-on collisions
View SolutionA ball of mass 150 gm starts moving at 20m//s and is hit by a force which acts for 0.1 second. The impulsive force is:
View SolutionA force of 20 N acts on a body for 2 micro second. Calculate the impulse. If the mass of the body is 1 g, calculate the change of velocity.
View SolutionTwo point masses are connected the light rod of length and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
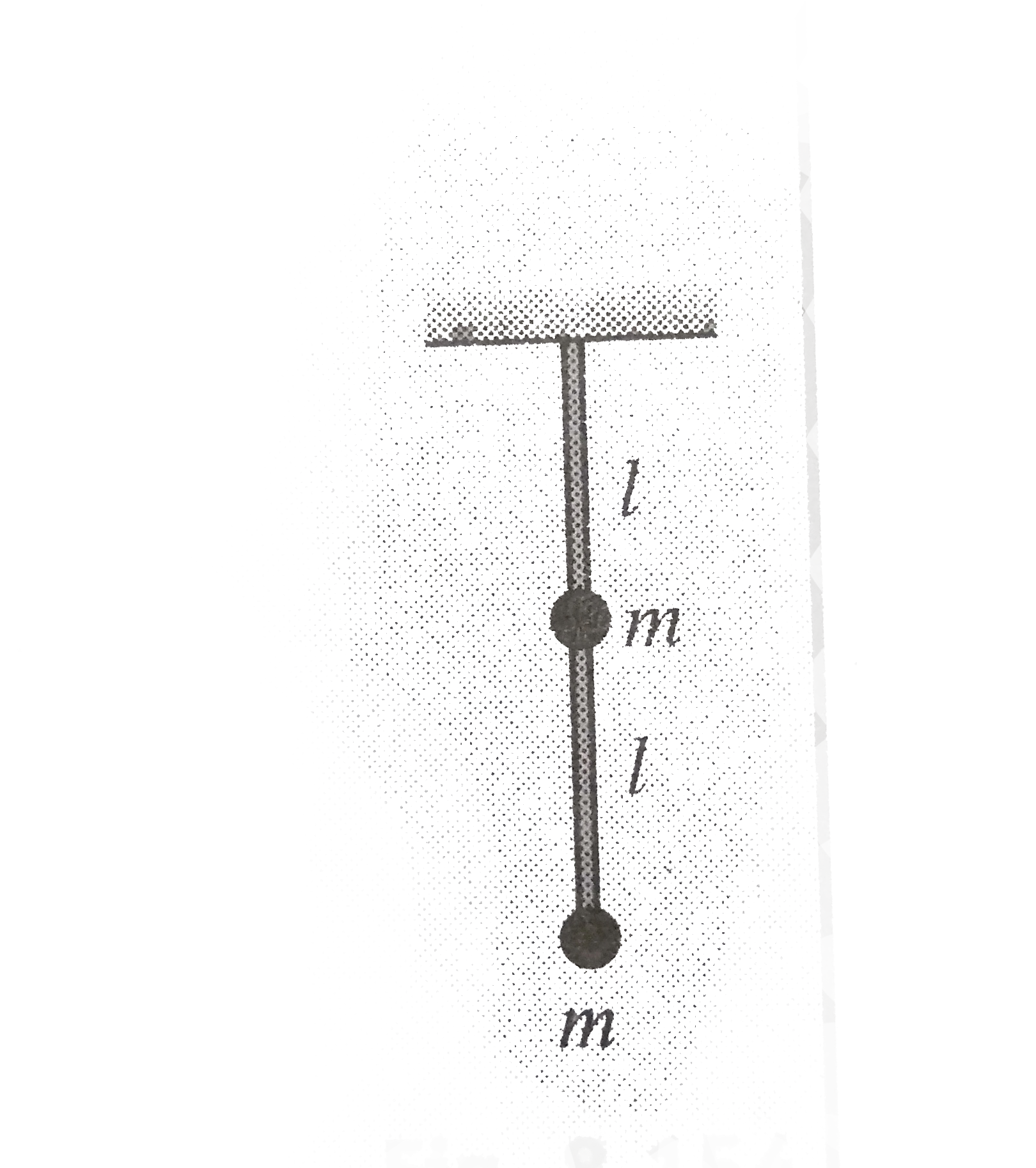
View SolutionTwo point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
View Solutionl लम्बाई व m द्रव्यमान की एक पतली एकसमान छड़ इसके एक सिरे से मुक्त रूप से कीलकित है। छड़ प्रारम्भ में क्षैतिज स्थिति में है एवं विरामावस्था से मुक्त की जाती है। जब छड़ ऊर्ध्वाधर होती है, इसको विरामावस्था में लाने के लिये एक आवेग Jआरोपित किया जाता है। (यह आवेग कीलकित द्वारा प्रदान किये किसी आवेग से अतिरिक्त है)

छड़ का कोणीय वेग उस क्षण पर क्या होगा जब यह ऊर्ध्वाधर स्थिति में पहुँचती है ?
View SolutionA uniform slender bar of mass and length supported by a firctionless and length supported by a firctionless pivot at is released from rest at its vertical position as shown the figure. Calculate the reaction at pivot when the bar just acquires the horizontal position shown dotted.

View SolutionA bob of mass m attached to an inextensible string of length l is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed omega rad/s about the vertical support. About the point of suspension
View SolutionA ball of mass 150g starts moving at 20 and hit by a force which acts on it for 0.1 second. Then the impulsive force is
View SolutionA ball of mass 150 g starts moving at 20 m/s and its hits by a force which acts on it for 0.1 sec. Then the impulsive force is:
View Solution