A skier mass m has the velocity vA = v0 at point A of the cross country course Although he tries hard not to lose velocity skiing uphill he reaches point B with only a velocity vB = 2 v0/5. Skiing downhill between point B and the finish C he again gains speed and reaches C with vC = 4 v0. Between B and C assume that a constant friction force acts due to the soft snow in this region; the drag force from the air on the skier can be neglected. Calculate the work done by the skier on the path from A to B here the friction force is negligible. Determine the coefficient of kinetic friction between B and C.
in order to calculate the work done by the skier on the path form A to B we use the work -energy theorem :Now we apply the work-energy theorem between points B and C where the work of the friction force is given by −RlBCThe result is valid only for µ ≥ 0
Related Solutions
Starting from point O facing West a man walks 4 km to reach point A. He turns right, walks 4 km and reaches point B. Then, he turns right walks 4 km and reaches point C. He takes right walks 3 km and reaches point D. He turns left, walks 4 km and reaches point E. Then, he turns right, walks 5 km and reaches point F. At point F, the man is facing ______ direction.
View SolutionA man in a boat crosses a river from point A. If he rows perpendicular to the banks he reaches point C in 10 min. If the man heads at a certain angle to the straight line AB (AB is perpendicular to the banks) against the current he reaches point B in 12.5 min. Find the width of the river w, the rowing velocity u, the speed of the river current v and the angle . Assume the velocity of the boat relative to water to be constant and the same magnitude in both cases.

View SolutionA man in a boat crosses a river from point A. If he rows perpendicular to the banks he reaches point C (BC = 120 m) in 10 min. If the man heads at a certain angle alpha to the straight line AB (AB is perpendicular to the banks) against the current he reaches point B in 12.5 min. Find the width of the river w, the rowing velocity u, the speed of the river current v and the angle alpha . Assume the velocity of the boat relative to water to be constant and the same magnitude in both cases.
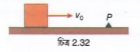
View Solutiona বাহু বিশিষ্ট একটি নিরেট ঘনক একটি মৃসণ অনুভূমিক তলের V0 ওপর বেগ নিয়ে যেতে যেতে P বিন্দুতে একটি পিনের সাথে ধাক্কা খেয়ে উলটে যায়। সেই মুহূর্তে তার কৌণিক বেগ হয়|
View SolutionA person starts from a point A and travels 3 km eastwards to B and then turns left and travels thrice that distance to reach C.
He again turns left and travels five times the distance he covered between A and B reaches his destination D. The shortest distance between the starting point and the destination is
View SolutionA point moves rectilinearly with deceleration whose modulus depends on the velocity of the particle as alpha=K sqrtv , where k is a positive constant. At the initial moment the velocity of the point is equal to V0. What is the distance will it takes to cover that distance.
View SolutionA particle crosses the topmost point C of a vertical circle with critical speed then the ratio of velocities at points A , B and C is

View SolutionA particle crosses the topmost point C of a vertical circle with critical speed , then the ratio of velocities at points A, B and C is

View SolutionA,B and C are three collinear points. B lies between A and C. A car stands on point A has reached to B after 3 seconds. If the angle of elevation of a pole of height 10m at C from the point A is and from B is , then velocity of the car is (given that acceleration of car is constant).
View SolutionA person starts from point A and reaches point C which is the midpoint of BD. If he takes four seconds time, then determine
(a) the average speed
(b) the average velocity.

View SolutionDirection: Study the following information carefully and answer the given question. Sahil starts from Point A and walks 8 m in south and reaches point B, then turns towards his left and walks 4 m and reaches Point C, from point C he turns his right and walks 5 m and reaches Point D. From D he turns 8 m towards left and reaches to E. From E he again turns left and walk 5 m reaches to F again turn right and walk 4 m to reach point G. Finally he again turns to his left and walks 8 m and reaches Point H.
Point E is in which direction with respect to C?
View SolutionTwo spheres of radii R and 2R are charged to potential V0 and 2 V0 and are connected by a battery of emf V0 as shown in figure. When switch 'S' is closed then
View SolutionDirection: Study the following information carefully and answer the given question. Sahil starts from Point A and walks 8 m in south and reaches point B, then turns towards his left and walks 4 m and reaches Point C, from point C he turns his right and walks 5 m and reaches Point D. From D he turns 8 m towards left and reaches to E. From E he again turns left and walk 5 m reaches to F again turn right and walk 4 m to reach point G. Finally he again turns to his left and walks 8 m and reaches Point H.
What is the distance between A and H and H is in which direction with respect to A?
View SolutionAssertion: A pendulam is oscillating between points A , B and C . Acceleration of bob at points A or C is zero. Reason: Velocity at these points is zero.
View SolutionAssertion: A pendulam is oscillating between points A , B and C . Acceleration of bob at points A or C is zero. Reason: Velocity at these points is zero.
View SolutionA body u is thrown upwards at a velocity. It gives three points A, B and C respectively to the velocities. (u)/(2),(u)/(3) And (u)/(4) Crosses with The ratio of the distance between points A and B and the distance between points B and C (AB)/(BC) is
View SolutionMr. X runs a marathon starting from point A. He runs 5 km towards north and reaches point B. 3 After that he takes a right turn and runs 6 km to reach point C. He again takes a right turn and runs 8 km to reach point D. Then he takes a right turn and runs 10 km to reach point E. Then he takes a right turn and runs 6 km to reach point F. Again taking a right turn and running 1 km reaches the point G. Finally he again took a right turn and ran 3 km. reaches the point. The shortest distance between points C and A is:
View SolutionA stone thrown vertically up with velocity v reaches three points A, B and C with velocities respectively. Then is
View SolutionA stone thrown vertically up with velocity reaches three points A,B and C with velocities
and respectively.Then AB:BC is
View SolutionA stone thrown vertically up with velocity v reaches three points A, B and C with velocities and respectively. Then AB:BC is
View Solution