Find the area of the portion of the cylinder x2 + z2 = 4 that lies above the rectangle defined by −1 ≤x ≤1 0 ≤y ≤2
The part of the cylinder above the rectangle D = [−1 1] × [0 2] can be represented as the graph of the function Its surface area is given by the formula We have and therefore Thus we have to compute the integral Here we used the formula
Related Solutions
The area of the portion of the circle which lies inside the parabola is -
View SolutionFind the area of the regionn bounded by the curve y^2=x , the x-axis and the lines x= 1, x= 4 and which lies above x-axis.
View SolutionFind the area of the smaller portion of the circle cut off by the line
View SolutionFind the area of the smaller portion of the circle cut off by the line
View SolutionProve that the points are the vertices of a rectangle. Also find the area of the rectangle.
View SolutionFind the equations of the diagonals of a rectangle whose sides are x + 1 = 0, x - 4 = 0, y + 1 = 0 and y - 2 = 0.
View SolutionFind the positive value of 'a' for which the parabola y=x^(2)+1 bisects the area of the rectangle with vertices (0,0),(a,0),(0,a^(2)+1) and (a,a^(2)+1)
View Solution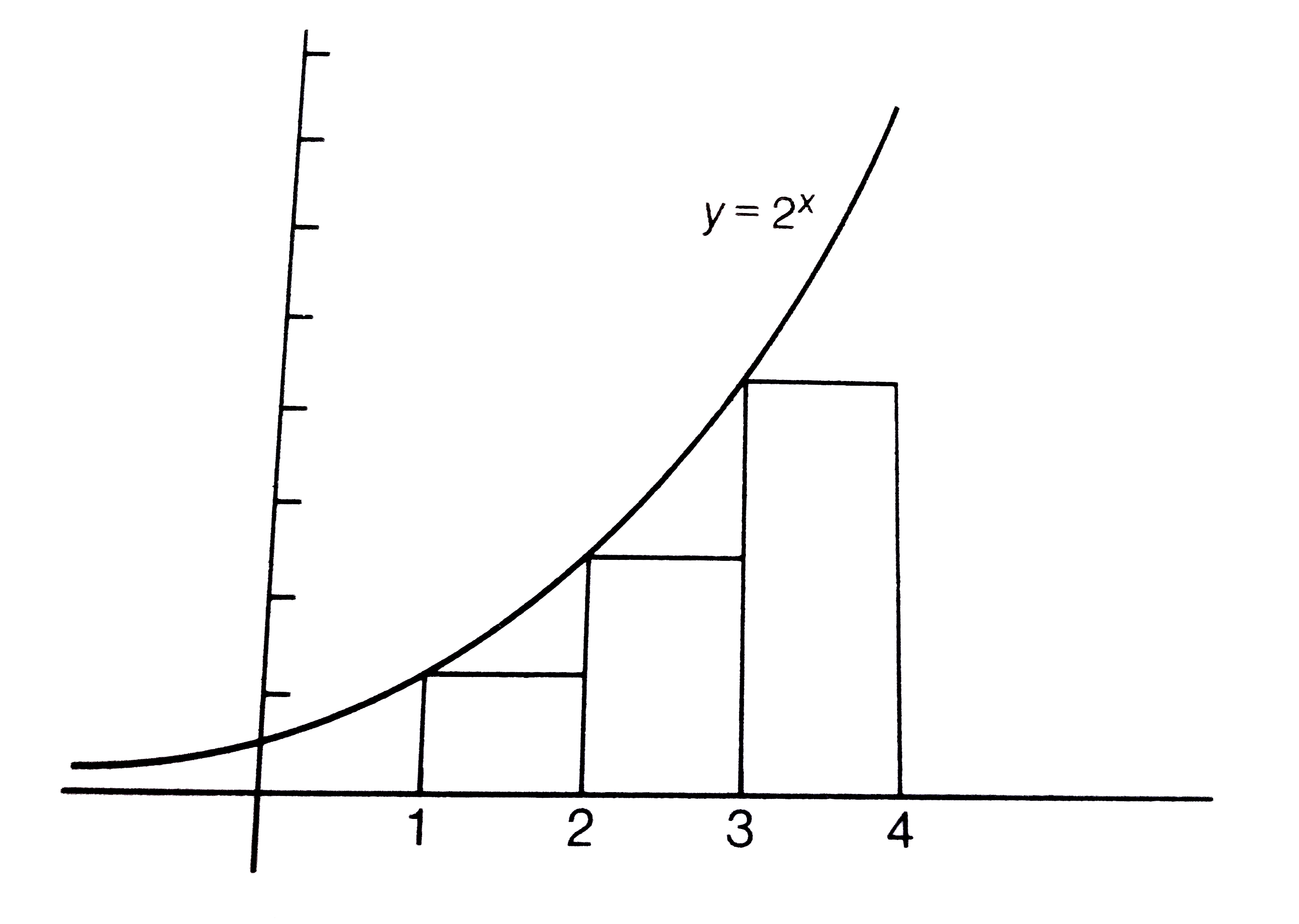
The figure above shows a portion of the graph of . What is the sum of the areas of the three inscribed rectangles shown?
View SolutionFind the area of the semi-portion of the circle
View SolutionFind the area of the semi-portion of the circle
View SolutionIf A is the mean of x,y and z and the additive inverse of (x+y)z is xy, then the mean of x2,y2 and z2 is
View Solutionव्रको और द्वारा घिरे हुए भाग का क्षेत्रफल ज्ञात कीजिए।
View SolutionThe curves y^2-x-1=0 And y^2 +x-1=0 Find the area of the area surrounded by.
View SolutionNo portion of the circle lies in the
View Solutionदीर्घवृत के अंतर्गत महत्तम क्षेत्रफल वाले आयत का क्षेत्रफल ज्ञात कीजिये ।
View Solutionz1, z2, z3 complex numbers such as | z1 | = | z2 | = | z3 | = | 1 / (z1) + 1 / (z2) + 1 / (z3) | = 1, then find the value of | z1 + z2 + z3 |.
View Solutionਪਹਿਲੀ ਚੌਥਾਈ ਵਿੱਚ ਨਾਲ ਘਿਰੇ ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ।
View SolutionEvaluate:
View SolutionIf the area of the ellipse is , then find the maximum area of rectangle inscribed in the ellipse.
View SolutionEvaluate the area bounded by the ellipse above the x-axis.
View Solution