If position in meter of a particle moving in straight line is given by x = t2 - 2t + 1 where t is time in second. The distance travelled by particle in first two second is a zero b 2 m c 4 m d 3 m
Correct option bExplanation:
Related Solutions
The position (in meters) of a particle moving on the x-axis is given by: x=2+9t +3t^(2) -t^(3) , where t is time in seconds . The distance travelled by the particle between t= 1s and t= 4s is m.
View SolutionThe position (in meters) of a particle moving on the x-axis is given by: where t is time in seconds . The distance travelled by the particle between t= 1s and t= 4s is m.
View Solution[" If position of particle moving in straight line is "],[" given by "x=(t^(3)-2t+10)m" ,where t is time in "],[" second,then acceleration of particle at "t=1],[" sec is "......]
View SolutionVelocity-time equation of a particle moving in a straight line is v=2t-4 for t le 2s and v= 4-2t for 1 gt 2s . The distance travelled ( in meters) by the particle in the time interval from t=0 to t=4s is 4k. The value of 'k' is ( Here t is in second and v in m/s) :
View SolutionA particle moves in a straight line and its velocity v at time t seconds is given by cm/sec. Find the distance travelled by the particle during the first 5 second after the start.
View SolutionA particle is moving in a striaght line and at a given time, its displacement is S = t^(3) - 6t^(2) + 9t , where t is in seconds and S is in meter . The total distance travelled by the particle during the first five seconds is
View SolutionA particle is moving in a striaght line and at a given time, its displacement is S = t^(3) - 6t^(2) + 9t , where t is in seconds and S is in meter . The total distance travelled by the particle during the first five seconds is
View SolutionDisplacement of a particle x =(t-2)^(2) Is denoted by, where x is in meters and t is in seconds, then the distance traveled by the particle in the first 4 seconds will be
View SolutionThe speed function of the particle along a straight line x=(2t-3)^(2) Is expressed as, where x is in meters and t is in seconds. (a) Find the position, velocity and displacement at t = 2 seconds. (b) Find the velocity of the particle at the origin.
View Solutionएक सरल रेखा में गतिमान कण किसी क्षण पर स्थिति निम्नलिखित सूत्र द्वारा दी जाती है :
जहाँ मी/से तथा मीटर है x मीटर में तथा t सेकण्ड में है ज्ञात कीजिए :
सेकण्ड सेकण्ड तथा सेकण्ड पर कर की स्थिति |
View Solutionসরলরেখায় গতিশীল একটি কণার t সেকেন্ডে সরণ x সেমি হলে হয় । যখন বস্তুকণার ত্বরণ শূন্য হবে, সেই সময় বস্তুকণা যে দূরত্ব অতিক্রম করবে তা হল-
View SolutionA particle moves along a straight line. At a time (in seconds) the distance (in meter) of the particle is given by . How long would the particle travel before coming to rest ?
View SolutionA particle moves along a horizontal line such that its equation of motion is , s in meters and t in second.
Find the total distance travelled by the particle in the first 2 seconds.
View SolutionA particle moves in a straight line such that the displacement x at any time t is given by x=6t^(2)-t^(3)-3t-4 . X is in m and t is in second calculate the maximum velocity (in ms^(-1)) of the particle.
View SolutionA particle is moving along a straight line in parallelism. In t seconds the velocity of the particle varies from 10 m / s to 20 m / s and at that time the particle travels a distance of 13500 cm. What is the value of t?
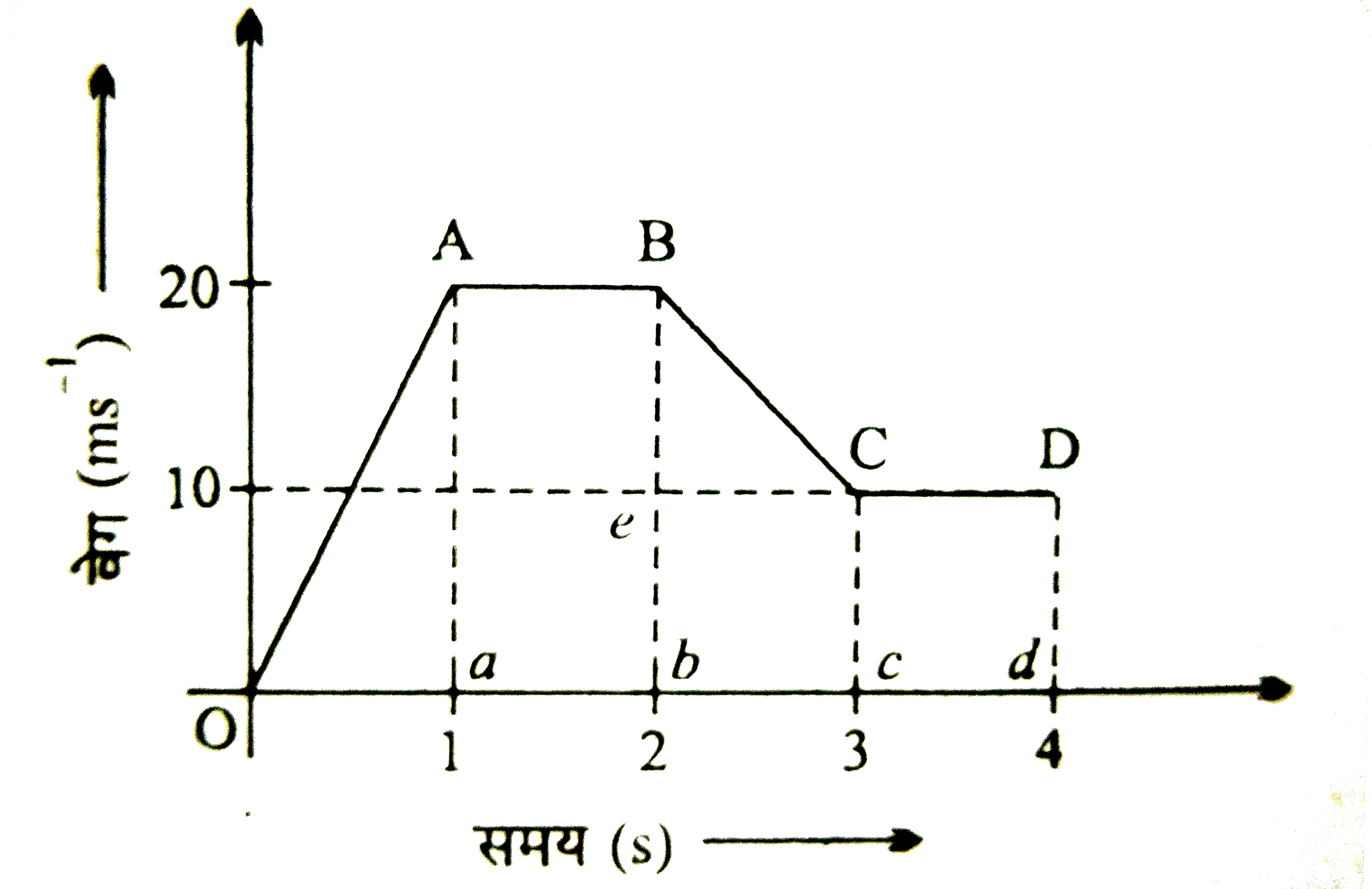
View Solutionसरल रेखा में गतिमान एक कण का वेग समय ग्राफ नीचे दिया गया है। पहले चार सेकंड में कण द्वारा तय दुरी की गणना कीजिए ।
View SolutionA particle is moving with an acceleration given by, ; where time t is in seconds and a is in . It is given that at t=0, u=0 and x=1 .Find distance travelled by particle from to .
View SolutionThe position of a particle along x-axis at time t is given by . The distance travelled by the particle (in 'm') in first 2 seconds is 's'. Fill '2s' in OME sheet.
View Solutionएक सरल रेखा में गति करते हुए कण का वेग-समय ग्राफ दर्शाए अनुसार है।
प्रथम 4 सेकण्ड में कण का विस्थापन व तय की गई दूरी ज्ञात कीजिए।
View SolutionThe displacement of a particle moving in a straight line, is given by s = 2t^2 + 2t + 4 where s is in metres and t in seconds. The acceleration of the particle is.
View Solution