Classify the following semileptonic decays of the D+1 869 = c bar d meson as Cabibbo-allowed Cabibbo-suppressed or forbidden in lowest order weak interactions. a D+ → K− + π+ + e+ + υe b D+ → π+ + π+ + e− + bar νe
For the charmed particles the selection rule for the Cabibbo allowed decay is ΔC = ΔS = ΔQ = ±1 and for the Cabibbo suppressed decays the selection rule is ΔC = ΔQ = ±1 ΔS = 0. Using these rules we infer that the decays are a Cabibbo allowed b forbidden
Related Solutions
The value of lim_(x to oo ) (log_(e)(log_(e)x))/(e^(sqrt(x))) is _________. (a) π/ 2 (b)0 (c)-π (d)π
View SolutionThe value of is _________. (a) π/ 2 (b)0 (c)-π (d)π
View SolutionEvaluate : . a) b) c) d)
View SolutionThere exists a triangle A B C satisfying the conditions (A) bsinA = a, A a, A > π/2 (C) bsinA > a, A < π/2 (D) bsinA < a, A < π/2, b < a
View SolutionThere exists a triangle satisfying the conditions
View Solutionlim x→0 ( sin x ) / x is equal to a. 1 b . π c. x d. π/180
View SolutionChoose the correct alternative answer for the following question: The ratio of circumference and area of a circle is 2:7. Find its circumference. (A) (B) ( C) (D)
View SolutionThe area of the region bounded by the ellipse is………a) sq.units b) sq.units c) sq.units d) sq.units
View SolutionThe value of is
a) πlog2
b) π/8log2
c) π/2log2
d) log2
View Solutiondx is equal to
a) π
b) π/2
c) 0
d) 2π
View Solution
View SolutionIf the sides of a triangle form successive terms of G.P. with common ratio then which of the following is correct? (a) B≥π/3C<π/3A < B < π/3
View SolutionIf the sides a , b , c of a triangle A B C form successive terms of G.P. with common ratio r(>1) then which of the following is correct? (a) A >pi/3 ' (b) B≥π/3 '(c) C<π/3 '(d) A < B < π/3
View SolutionIf and are not coplanar vectors and then K = ….
View SolutionA uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate . Loop 1 of radius R r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is
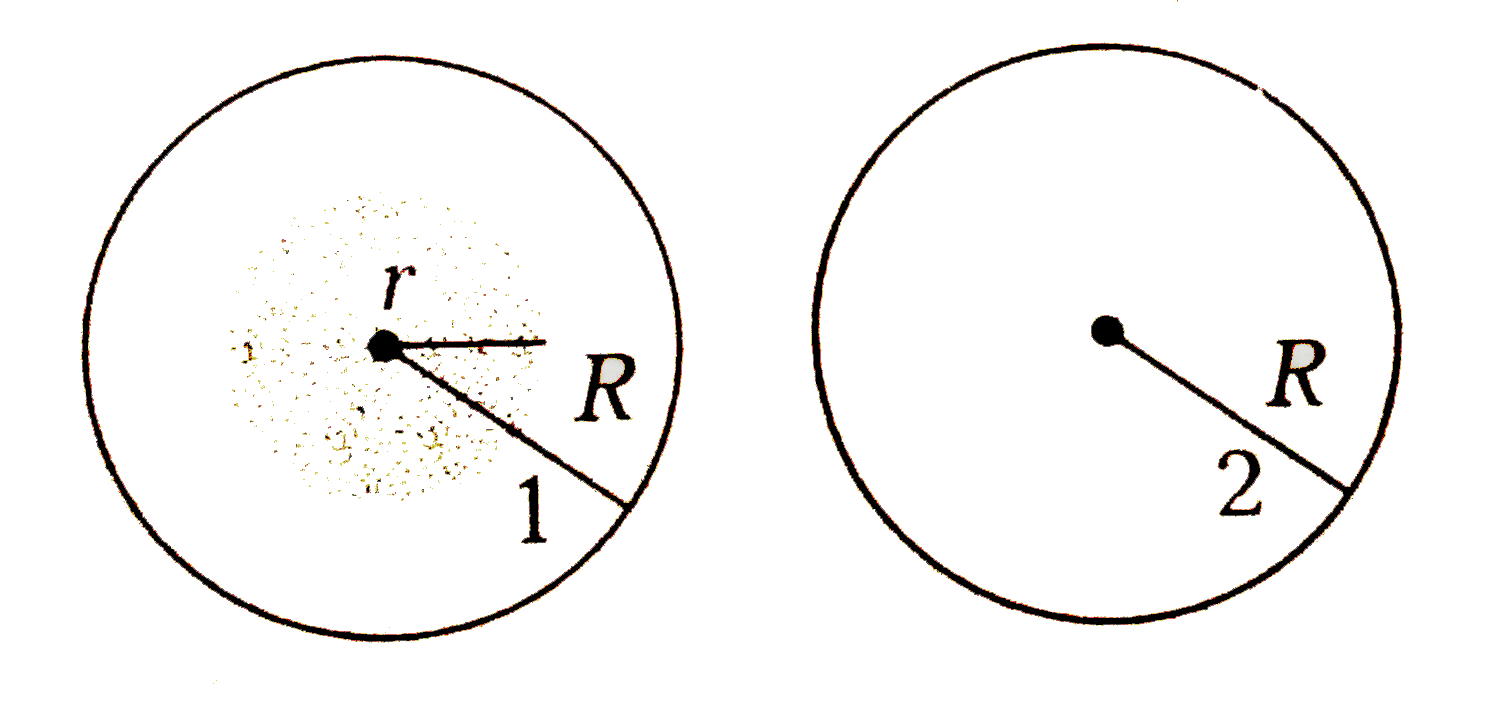
Zero in loop 1 and zero in loop 2
− d B d t π r 2 in loop 1 and − d B d t π 2 in loop 2
− d B d t π R 2 in loop 1 and zero in loop 2
− d B d t π r 2 in loop 1 and zero in loop 2
View SolutionThe number of ordered pairs (α,β), where α,β∈(−π,π) satisfying cos (α−β)=1 and cos(α+β)=1/e is
View SolutionThe number of ordered pairs (α,β), where α,β∈(−π,π) satisfying cos (α−β)=1 and cos(α+β)=1/e is
View SolutionIf cos(α−β)=1 and cos(α+β)= 1/e , where α, β∈[−π,π]. Then number of ordered pairs of (α,β) is
View SolutionEvaluate
View Solution13 . a r e ∈ H . P . t h e n : A ) B ) C ) D )
View Solution