A ball is thrown straight downward from the top of a tall building. The initial speed of the ball is 10m/s. It strikes the ground with a speed of 60m/s. How tall is the building?
I’ll assume that the acceleration due to gravity is 10m/s2 . The equation for the ball’s velocity in the downward direction is: vt = at + v0.HereSolving this for tf we get: The total distance traveled will be Here x0 = 0 and we get
Related Solutions
A ball is thrown upward from the top of a 25.0 m tall building. The ball's initial speed is 12.0 m/s. At the same instant, a person is running on the ground at a distance of 31.0 m from the building. What must be the average speed of the person if he is to catch the ball at the bottom of the building ?
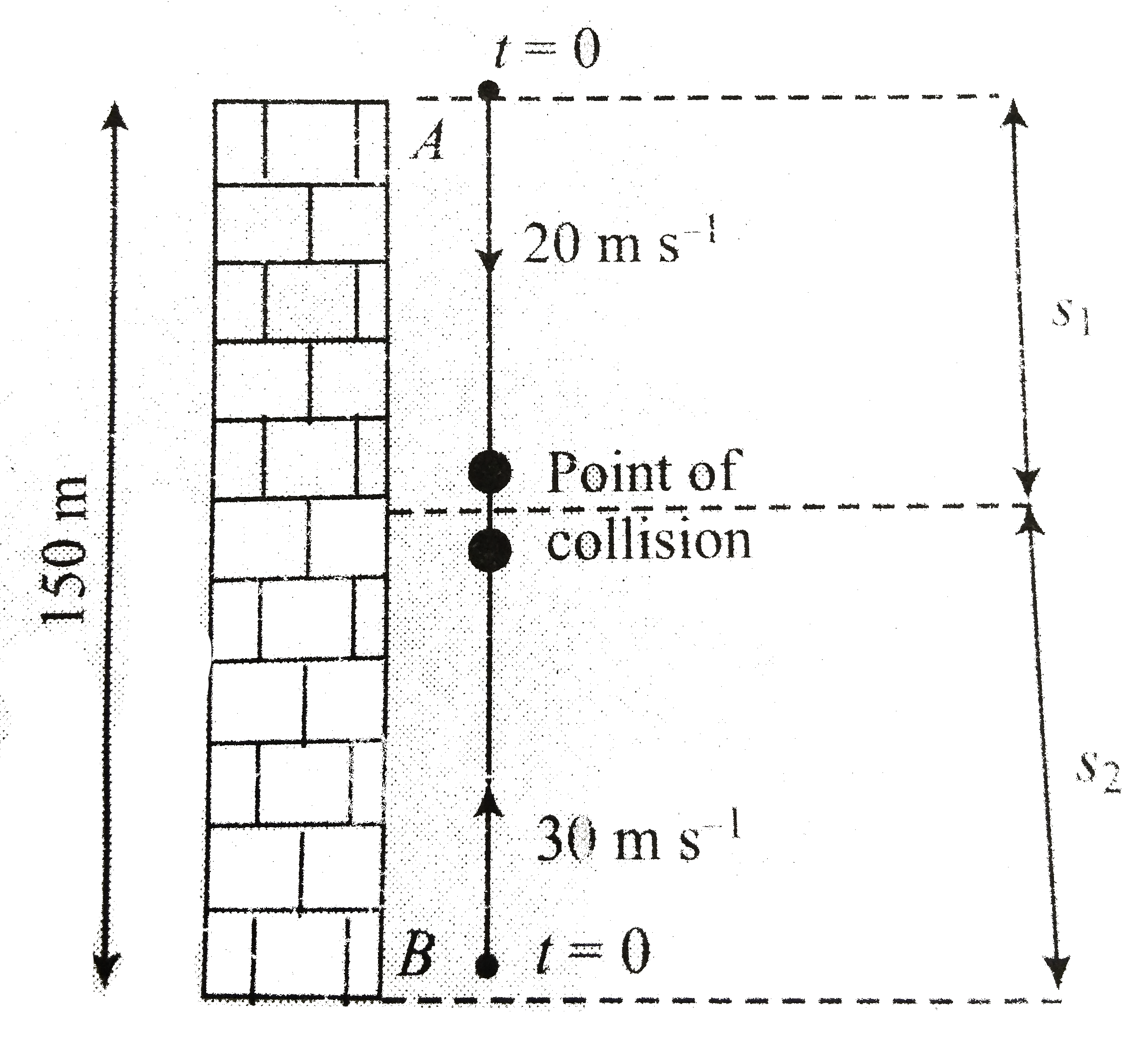
View SolutionA ball is thrown downwards with a speed of 20m//s from top of a building 150m high and simultaneously another ball is thrown vertically upwards with a speed of 30m//s from the foot of the building . Find the time when both the balls will meet . (g=10m//s^(2))
View SolutionTwo tall buildings are 40m apart. A ball thrown horizontally from a window 145m above the ground in one building is to enter a window 22.5m above the ground in the other building.The speed of the ball should be (A) 6m/s (B) 8m/s (C) 10m/s (D) 12m/s
View SolutionA ball is thrown vertically upward from the top of a building 96feet tall with an initial velocity of 80feet per second. The distance S (in feet )of the ball from the ground, after t seconds is . After how many seconds does the ball strike the ground.
View SolutionTwo tall buildings are 40m apart A ball thrown horizontally from a window 145m above the ground in one building is to enter a window 22.5m above the ground in the other building. The speed of the ball should be
View SolutionFrom the top of a building , a ball is thrown horizontally. The ball strickes the ground after 5 s at an angle of to the horizontal. Calculate the speed with which the ball was projected .
View SolutionA ball is thrown downwards with a speed of , from the top of a building high and simultaneously another ball is thrown vertically upwards with a speed of from the foot to the building . Find the time after which both the balls will meet. (g=10 m s^(-2))
 .
.
View SolutionTwo tall buildings are 40 m apart. With what speed should a ball be thrown horizontally from a window in a building 145 m above the ground, so that it enters a window in another building 22.5 m above the ground?
View SolutionA ball is thrown with a velocity of from the top of a building 200m high . The ball makes an angle of with the horizontal . Calculate the distance from the foot of the building where the ball strikes the ground .
View SolutionTwo tall buildings are 40m apart. With what speed must a ball be thrown horizontally from a window 145 m above the ground in one building, so that it will enter a window 22.5 m above the ground in other ?
View SolutionTwo tall buildings are 100 m apart with what speed must a ball be thrown horizontally from the window 500 m above the ground in one building. So that it will enter a window 100 m above the ground in the other ?
View SolutionA ball is dropped from the top of an 80 m high tower After 2 s another ball is thrown downwards from the tower. Both the balls reach the ground simultaneously. The initial speed of the second ball is
View SolutionA ball is tossed from the window of a building with an initial velocity of at an angle of below the horizontal . It strikes the ground 3 s later. From what height was the ball thrown? How far from the base of the building does the ball strike the ground?
View SolutionA ball is tossed from the window of a building with an initial velocity of 8 ms^-1 at an angle of 20^@ below the horizontal . It strikes the ground 3 s later. From what height was the ball thrown? How far from the base of the building does the ball strike the ground?
View SolutionA ball is dropped from the top of a building of height 80 m. At same instant another ball is thrown upwards with speed 50 m/s from the bottom of the building. The time at which balls will meet is
View SolutionA ball is dropped from the top of a building of height 80 m. At same instant another ball is thrown upwards with speed 50 m/s from the bottom of the building. The time at which balls will meet is
View SolutionIf a ball is thrown up with a velocity v from the top of a building the ball reaches the ground with a velocity 3u. Find the height of the building.
View SolutionA ball is thrown vertically upwards with the speed of 19.6 ms^(-1) from the top of building and reaches the earth in 6 s. Find the height of the building .
View SolutionA ball is thrown from the top of a building with a velocity of 10 m/s and returns with a velocity of 30 m/s to the ground. Find the height of the building.
View Solutionकिसी मीनार के शिखर से किसी गेंद को 20m/s के वेग से ऊर्ध्वाधर अधोमुखी फेंका गया हैं कुछ समय पश्चात यह गेंद धरती से 80m/s के वेग से टकराती है। इस मीनार की ऊंचाई होगी
View Solution