A bar of mass m length is in pure translatory motion with its centre of mass velocity . It collides with and sticks to another identical bar at rest as shown in figure. Assuming that after collision it becomes one composite bar of length 2l the angular velocity of the composite bar will be.A 3v/4l anticlockwiseB 4v/3l anticlockwise C 3v/4l clockwiseD 4v/3l clockwise
Correct option A 3v/4l anticlockwiseExplanation:by conservator angular momentum aboutjoint
Related Solutions
A bar of mass M and length L is in pure translatory motion with its centre of mass velocity V. It collides with and sticks to a second identical bar which is intially at rest. (Assume that it becomes one composition bar of length 2 L). The angular velocity of the composite bar will be 3V/xL counter clockwise where 'x' is
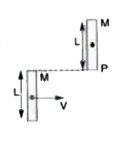
View SolutionA bar of mass m and length l is in pure translational motion with its centre of mass moving with a velocity v. It collides and sticks to another identical bar at rest as shown in the figure. Assuming that after the collision the system of the two bars becomes one composite bar of length 2l, then the angular velocity of the composite bar will be
View SolutionA bar of mass m and length l is in pure translational motion with its centre of mass moving with a velocity v. It collides and sticks to another identical bar at rest as shown in the figure. Assuming that after the collision the system of the two bars becomes one composite bar of length 2l, then the angular velocity of the composite bar will be
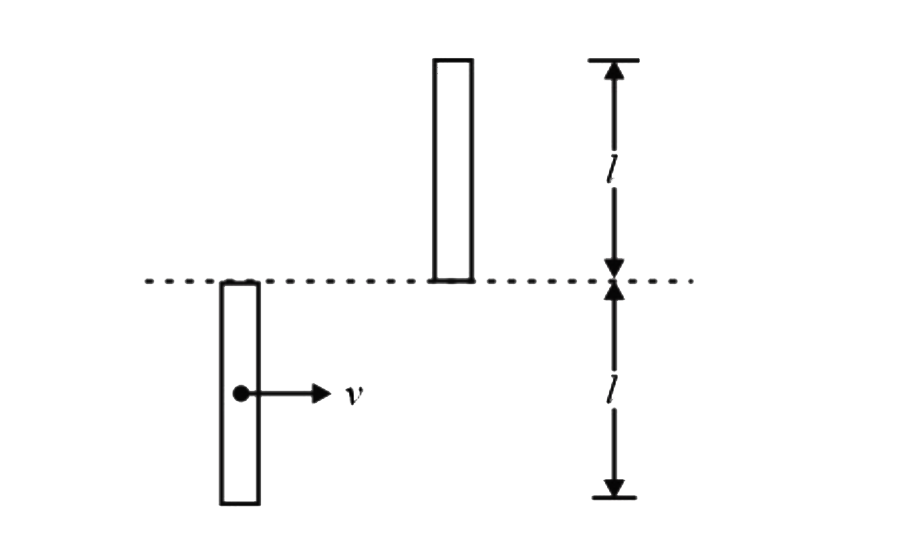
View SolutionA bar of mass M and length L is in pure traslatory motion with its of mass velocity V . It collides with and sticks to a second identical bar which is initially at rest . ( Assume that it bocomes one composite bar of length 2L) . The angular velocity of the composite bar will be
View SolutionA bar of mass M and length L is in pure traslatory motion with its of mass velocity V . It collides with and sticks to a second identical bar which is initially at rest . ( Assume that it bocomes one composite bar of length 2L) . The angular velocity of the composite bar will be
View SolutionA bar of mass 'm' length 'l' is in pure translatory motion with its centre velocity 'v' It collides with another identical bar which is in rest and sticks to it.
Assume that after the collision it becomes one system, then the angular velocity of the system after the collision is.
 .
.
View SolutionA bar of mass 'm' length 'l' is in pure translatory motion with its centre velocity 'v' It collides with another identical bar which is in rest and sticks to it.
Assume that after the collision it becomes one system, then the angular velocity of the system after the collision is.
 .
.
View SolutionTwo particles and of mass each hit the ends of a rigid bar of mass and length inelastically from opposite sides the speeds and perpendicular to the rod. The bar is kept on a smooth horizontal plane (as shown). Find the linear and angular speed of the system (barparticle).

View SolutionA uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving with the same horizontal speed 2v and v respectively, strike the bar as shown in the figure and stick to the bar after collision. Denoting angular velocity (about the centre of mass), total energy, and centre of mass velocity after collision by omega , E and v_(C) respectively, we have after collision
View SolutionA rod of mass m and length l is moving at a net translational speed with v velocity along the center of mass. As shown in the figure, it collides with and clings to another composite rod which is in resting state. Assuming that the body of the two rods becomes a joint rod of length 2l after the impact, what will be the angular velocity of the joint rod?
View SolutionA uniform bar of length and mass lies on a smooth horizontal table. Two point masses and moving in the same horizontal plane with speeds and , respectively, strike the bar (as shown in the figure) and stick to the bar after collision. Denoting angular velocity (about the centre of mass), total energy and centre of mass velocity by , and , respectively, we have after collision
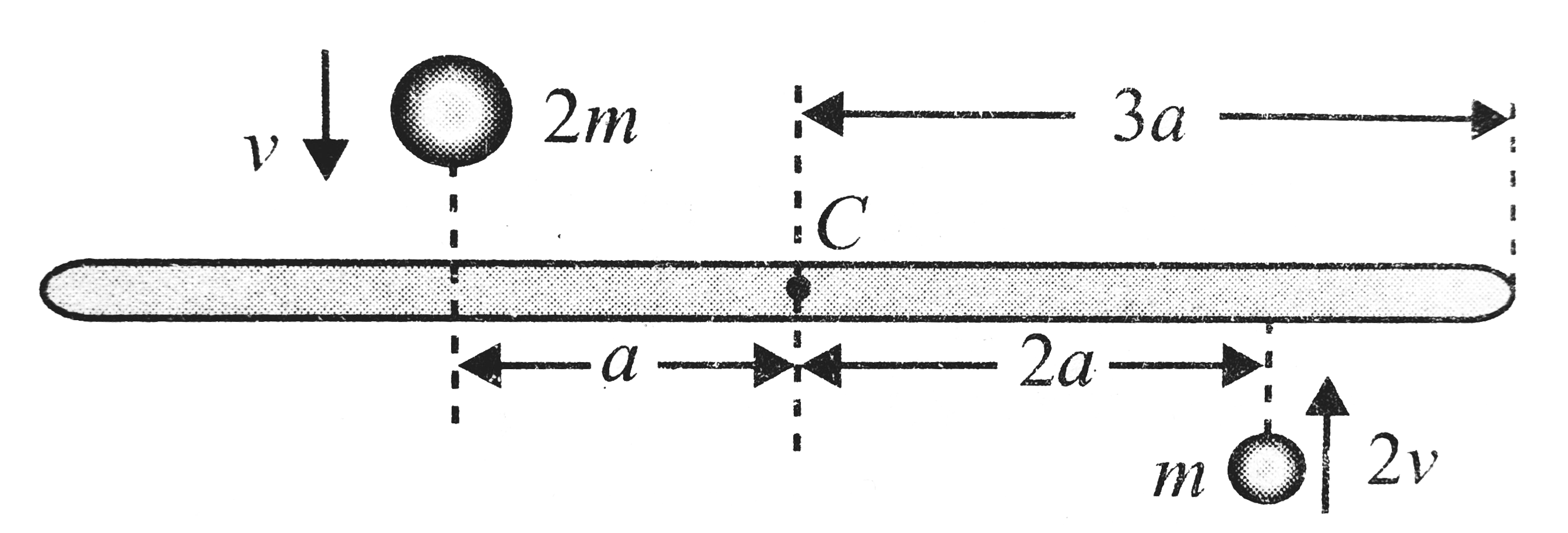
View SolutionA uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speeds 2v and v respectively, strike the bar (as shown in figure) and stick to the bar after collision. Calculate (a) velocity of the centre of mass (b) angular velocity about centre of mass and (c) total kinetic energy, just after collision.
View SolutionA uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speeds 2v and v , respectively, strike the bar (as shown in the figure) and stick to the bar after collision. Denoting angular velocity (about the centre of mass), total energy and centre of mass velocity by omega , E and V_(C) , respectively, we have after collision
View SolutionA uniform bar of length (6a) and mass (8m) lies on a smooth horizontal table. Two point masses (m) and (2m) moving in the same horizontal plane with speeds (2v) and (v) respectively strike the bar as shown in the figure and stick to the bar after collision. The rotational kinetic energy of the system after the collision is
View SolutionA thin uniform bar of length L and mass 8m lies on a smooth horizontal table .Two point masses m and 2 m are moving in the same horizontal plane from opposite sides of the bar with speeds 2v and v respectively .The masses stick to the bar after collision at a distances respectively from the center of the bar if the bar starts rotating about its center of mass as result of collision the angular speed of the bar will be
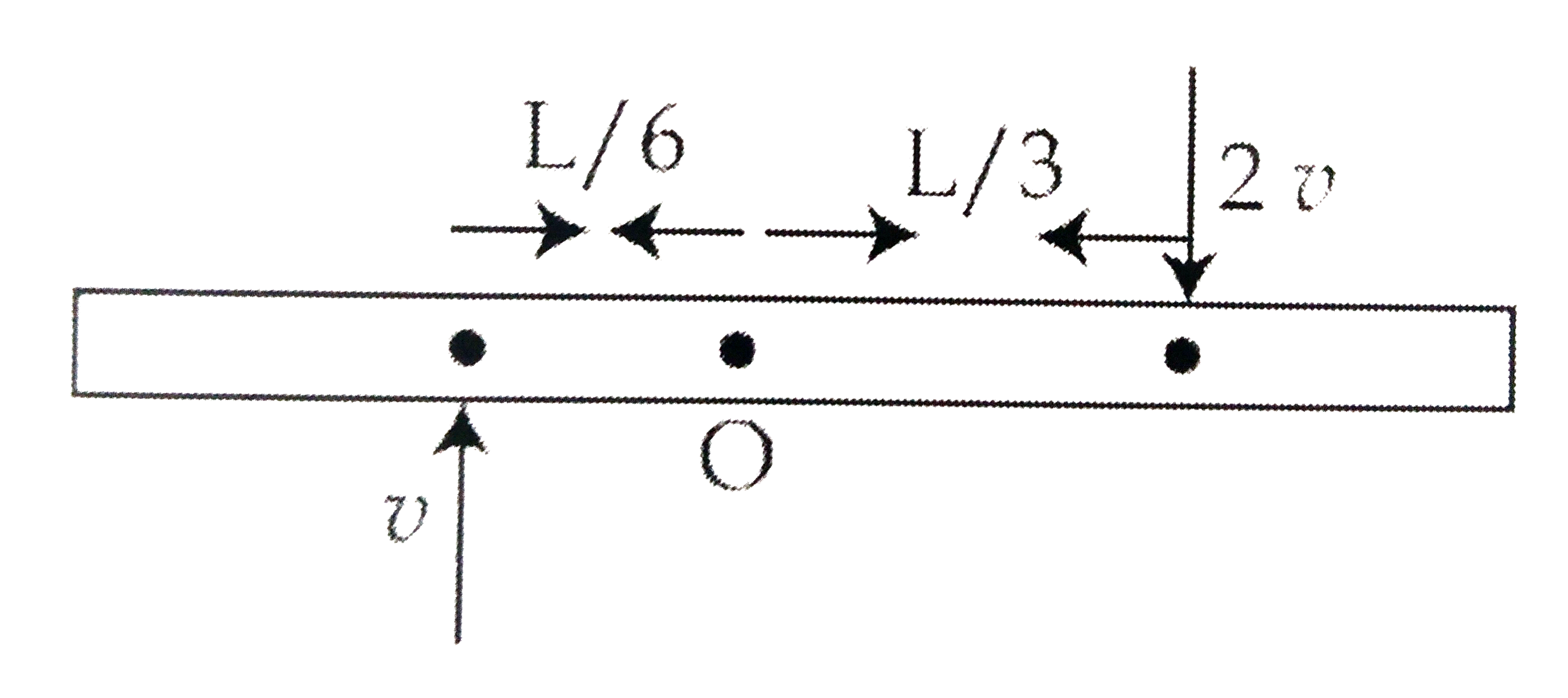
View SolutionA thin uniform bar of length L and mass 8m lies on a smooth horizontal table .Two point masses m and 2 m are moving in the same horizontal plane from opposite sides of the bar with speeds 2v and v respectively .The masses stick to the bar after collision at a distances respectively from the center of the bar if the bar starts rotating about its center of mass as result of collision the angular speed of the bar will be

View SolutionA uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speed 2v and v, respectively, strike the bar [as shown in the fig.] and stick to the bar after collision. Denoting angular velocity (about the centre of mass), total energy and centre of mass velocity by , E and respecitvely, we have after collison
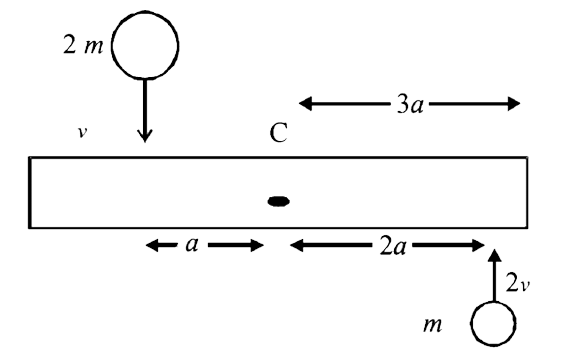
View SolutionA uniform bar of length 6a and mass 8 m lies on a smooth horizontal table. Two point-masses m and 2m moving in the same horizontal plane with speeds 2v and v respectively strike the bar as shown in Fig, and stick to the bar after collision.
View SolutionA uniform thin bar is of mass 4 kg and length 2 m. the M.I. of bar about an axis passing through its centre and perpendicular to the length is
View SolutionA uniform bar AB of length has been placed on a horizontal smooth table of width 5 a as shown in the figure. Length 2a of the bar is overhanging. Mass of the bar is 4m. An insect of mass m is sitting at the end A of the bar. The insect walks along the length of the bar to reach its other end B.
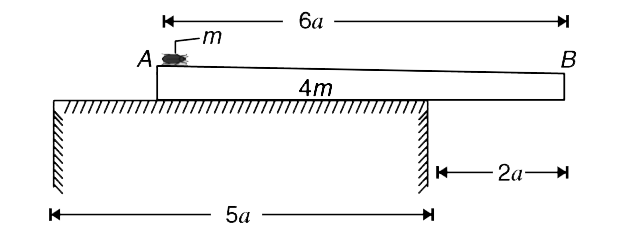
(a) Will the bar topple when the insect reaches end B of the bar ?
(b) After the insect reaches at B, another insect of mass M lands on the end A of the bar. Find the largest value of M which will not topple the bar.
View Solution