Let the angle between two nonzero vectors A and B be 120° and its resultant be C. a C must be equal to I A —B I b C must be less than I A —B c C must be greater than I A —B I d C may be equal to I A —B|.
c C must be greater than I A —B I
Related Solutions
If is equal to a. b. c. d. none of these
View SolutionIf is equal to a. b. c. d. none of these
View SolutionIf is equal to a. b. c. d. none of these
View SolutionIf is equal to a. b. c. d. none of these
View SolutionLet . If d is a unit vector such that then d equals
View SolutionA + B means A is greater than B. A B means A is greater than or equal to B.
A = B means A is equal to B.
A @ B means A is smaller than B.
A B means A is smaller than or equal to B.
Statements: A @ B, C A, C + D
Conclusions: I. C @ B II. B + D
View SolutionLet and c be a vectors such that and the angle between c and . Then a. c is equal to
View SolutionLet a= 2hat(i)+ hat(j) -2hat(k) , b=hat(i) +hat(j) and c be a vectors such that |c-a| =3, |(axxb)xx c|=3 and the angle between c and axx b" is "30^(@) . Then a. c is equal to
View SolutionLet and c be a vectors such that and the angle between c and . Then a. c is equal to
View SolutionLet and c be a vectors such that and the angle between c and . Then a. c is equal to
View SolutionLet a = i- 2j + k and b = i-j+k be two vectors. If c is a vector such that b x c = b x a and c.a = 0, then c . b is equal to:
View Solution(a) a- i ,b-iii,c-ii (b) a-iii,b-ii,c- i (c) a-ii,b-iii,c- i (d) a-ii,b- i ,c-iii
View Solution(a) a- i ,b-iii,c-ii (b) a-iii,b-ii,c- i (c) a-ii,b-iii,c- i (d) a-ii,b- i ,c-iii
View SolutionIf are idempotent matrices, then is equal to a. b. c. d.
View SolutionIf are idempotent matrices, then is equal to a. b. c. d.
View SolutionIf are idempotent matrices, then is equal to b. c. d.
View SolutionIf , then
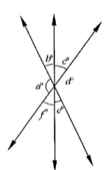
View SolutionIn Figure, which of the following statements must be true? (i) (ii) (iii) (a) (i) only (b) (ii) only (c) (iii) only (d) (ii) and (iii) only
View SolutionIf a+ I/b=1 and b+I/c=1, then value of abc is equal to
View SolutionWrite the value of .
View Solution