The principal cross-section of a prism is an equilateral triangle. A ray is perpendicular to one of its faces. What will be the path of this ray for different values of the refractive index of the material from which the prism is made?
If n < 1.15 the ray is refracted at the second face and leaves the prism. Atherwise it is internally reflected and leaves through the third face without refraction.
Related Solutions
A ray is incident normally on the refracting face of the prism made of material of refractive index . Complete the path of ray through the prism. From which face will the ray emerge and at what angle ? Justify your answer.
View SolutionA ray of light incident on one face of an equilateral prism at 60^@ enters and leaves prism symmetrically. Refractive index of prism material is
View SolutionA ray PQ incident normally on the refracting face BA is refracted in the prism BAC made of material of refractive index 1.5 . Complete the path ray through the prism. From which face will the ray emerge ? Justify your answer.
View SolutionA ray incident normally on the refracting face is refracted in the prism made of material of refractive index . Complete the path ray through the prism. From which face will the ray emerge ? Justify your answer.
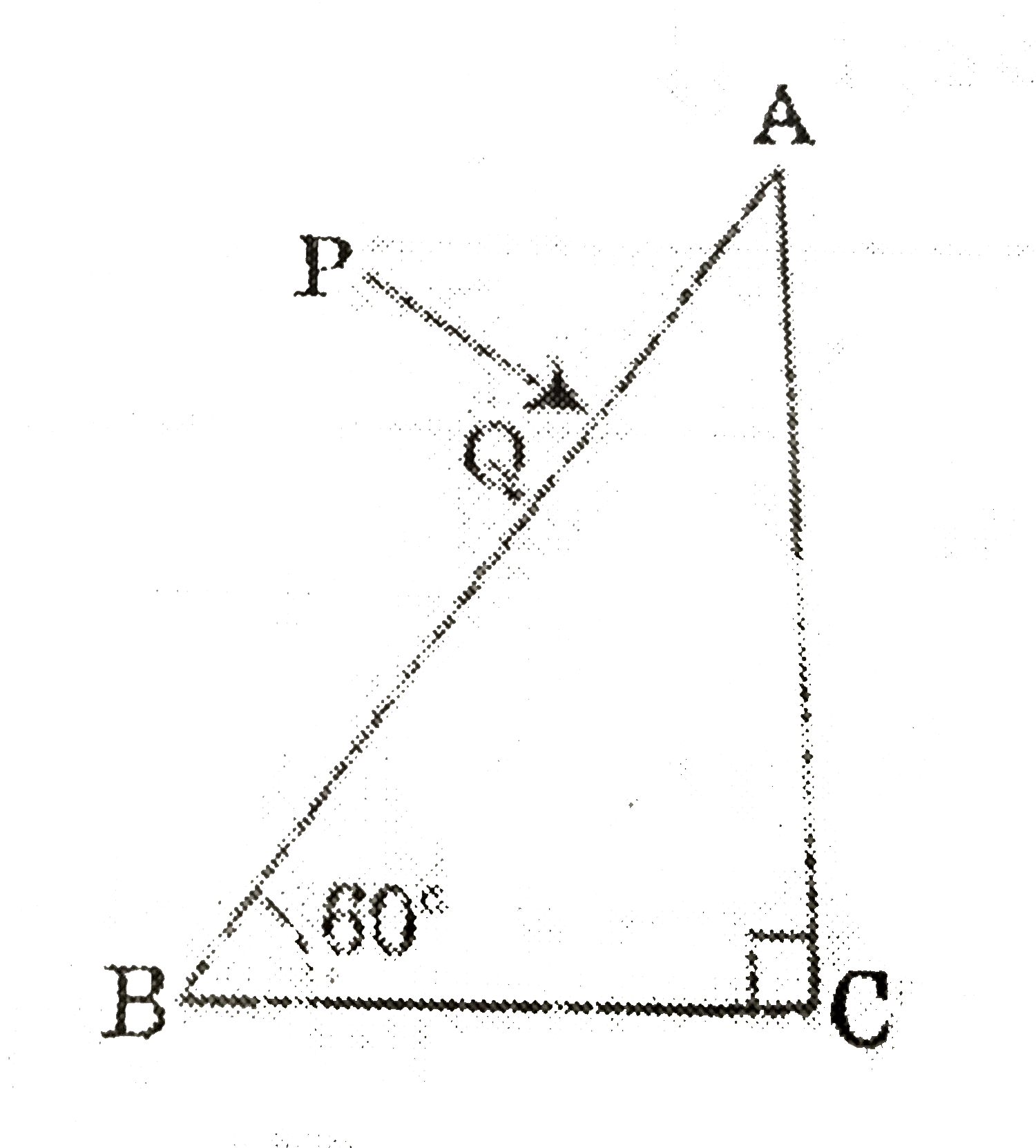
View SolutionA ray of light is incident normally on one face of a prism of refracting angle A. After travelling through prism, the ray emerges from the second refracting surface making an angle of deviation of . The refractive index of the material of prism is
View SolutionA monochromatic ray of light is incident normally on one of the refracting surfaces of a prism . The emergent ray grazes the second refracting surface . What is the angle of the prism if the refractive index of the material of the prism is ?
View SolutionThe refractive angle of prism is A. A ray is incident normally on one of the refracting faces of a prism and emerges out. If D be the deviation of the ray then refractive index of the material of the prism is—
View SolutionA monochromatic ray of light is incident normally on one of the refracting surfaces of a prism . The emergent ray grazes the second refracting surface . What is the angle of the prism if the refractive index of the material of the prism is ?
View SolutionA ray of light incident at an angle 90° with the face of an equilateral prism passes symmetrically. Calculate the refractive index of the material of the prism
View SolutionA ray of light incident at an angle 90° with the face of an equilateral prism passes symmetrically. Calculate the refractive index of the material of the prism
View SolutionWhen a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism
View SolutionA ray of light is incident normally on one refracting surface of an equilateral prism. If the refractive index of the material of the prism is 1.5, then
View SolutionWhen a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5 )
View SolutionWhen a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5
View SolutionThere is an equilateral prism of material of refractive index 1.5. Light ray is incident normally on its surface. What will be the angle of deviation of ray ?
View SolutionAn equilateral prism is made of material with refractive index 1.73. A light ray incident at an angle i on it refract and moves parallel to the base of the prism. Find the value of i.
View SolutionFor an equilateral prism, it is observed that when a ray strikes grazingly at one face, it emerges grazingly at the other face, its refractive index will be
View SolutionFor an equilateral prism, it is observed that when a ray strikes grazingly at one face, it emerges grazingly at the other face, its refractive index will be
View SolutionA light ray falls perpendicular on one face of an equilateral prism having refractive index .The angle of deviation is :
View SolutionThe refracting angle of a glass prism is 30^@. A ray is incident onto one of the faces perpendicular to it. Find the angle delta between the incident ray and the ray that leaves the prism. The refractive index of glass is mu=1.5.
View Solution