A glass ball has a mirror-like inner surface. The radius of the ball is 36 cm. A point source S is placed at a distance R/2 from the centre of the ball and sends light towards the furthest part of the ball. Where will be the image of the source after two reflections i.e. from the far and near wall of the ball? How will the position of the image change if the source sends out light towards the nearer wall?
Answer: At a distance 5R/6 from the near wall; at a distance R/2 from the far wall.Explanation:To solve the problem it is necessary in the first case to calculate first the position of image A1 formed by the far wall and then considering it as a source find the image A2 of this source formed by the other wall.To determine the position of images A1 and A2 graphically one should consider the path of some arbitrary ray SB Fig. travelling from the source at a small angle to the optical axis. To determine the direction of this ray after the first reflection at point B it is necessary to produce another optical axis as such that ray SB intersects it at the focus. The reflected ray BC is parallel to this axis. Image A1 lies at the point of intersection of ray BC and the principal optical axis. After the second reflection from the near wall at point C the ray should be parallel to an optical axis bb through the focus of which the ray BC passes. Image A2 lies at the point of intersection of ray CA2 and the principal optical axis. The order of carrying out the graphical construction in the second case is illustrated in Fig..
Related Solutions
The internal surface of the walls of a sphere is specular (i.e. reflecting). The radius of the sphere is R = 36 cm . A point source S is placed at a distance R//2 from the centre of the sphere and sends light to the remote part of the sphere. Where will the image of the source be after two successive reflection from the remote and then the nearest wall of the sphere ? How wil the position of the image change if the source sends light to the nearest wall first ? Consider paraxial rays.
View SolutionThe radius of a glass ball is 5 cm. There is an air bubble at 1cm from the centre of the ball and refractive index of glass is 1.5. The position of image viewed from surface near the bubble is.
View SolutionThe inner surface of the wall of a sphere is perfectly reflecting. Radius of the sphere is R. A point source S is placed at a distance from the centre of the sphere. Consider the reflection of light from the farthest wall followed by reflection from the nearest wall. Where is the image of the source? Consider paraxial rays only.
View SolutionOut of 4 identical balls of radius r, 3 balls are placed on a plane such that each ball touches the other two balls.The 4^(th) ball is placed on them such that this ball touches all the three balls. What is the distance of centre of 4^(th) ball from the plane?
View Solutionr त्रिज्या वाली 4 समान अभिन्न गेंदों में से 3 गेंदों को एक समतल पर इस प्रकार रखा गया है कि प्रत्येक गेंद अन्य दो गेंदों को स्पर्श करती है। चौथी गेंद को इन गेंदों पर इस प्रकार रखा गया है कि यह गेंद सभी तीनों गेंदों को स्पर्श करती है। चौथी गेंद के केंद्र कि समतल से दूरी, कितनी है ?
View SolutionAn uncharged ball of radius R is placed at a point in space and the region outside (from R to measured from centre of the ball) the ball is non-uniformly charged with a charge density where 'C' is a positive constant and r is the distance of a point measured from centre of the ball.
Electric field intensity at a distance x from centre of the ball is
View SolutionThe internal surface of the walls of a sphere is specular. The radius of the sphere is A point source S is placed at a distance from the cneter of the sphere and sends light to the remote part of the sphere. Where will the image of the source be after two successive reflections from the remote and then nearest wall of the sphere? How will the position of the image change if the source sends light to the nearest wall first?Consider paraxial rays.
View SolutionThe internal surface of the walls of a sphere is specular. The radius of the sphere is R=36cm. A point source S is placed at a distance R//2 from the cneter of the sphere and sends light to the remote part of the sphere. Where will the image of the source be after two successive reflections from the remote and then nearest wall of the sphere? How will the position of the image change if the source sends light to the nearest wall first?Consider paraxial rays.
View SolutionA ball is projected in a horizontal direction with a velocity of 10 m // s upwards in an 80 m deep well. How far the ball will fall in the bottom of the well (all the balls of the ball from the walls of the well are expected):
View SolutionA spherical ball of radius 3 cm is melted and recast into the spherical balls. The radii of two of these balls are 1.5 cm and 2 cm. Find the radius of the third balls.
View SolutionA spherical ball of radius is melted and recast into three spherical balls. The radii of two of these balls are and The radius of the third ball is
View SolutionIn an elastic collision between two billiard balls. The variation of potential energy is represented by the graph (here r is the distance between centres of the balls and R is radius of the ball)
View SolutionIn the elastic collision between two billiard balls. The variation of potential energy is represented by the graph (here r is the distance between centres of the balls and R is radius of the ball)
View SolutionIn the elastic collision between two billiard balls. The variation of potential energy is represented by the graph (here r is the distance between centres of the balls and R is radius of the ball)
View SolutionIn an elastic collision between two billiard balls. The variation of potential energy is represented by the graph (here r is the distance between centres of the balls and R is radius of the ball)
View SolutionAn uncharged ball of radius R is placed at a point in space and the region outside (from R to measured from centre of the ball) the ball is non-uniformly charged with a charge density where 'C' is a positive constant and r is the distance of a point measured from centre of the ball.
Electric potential at the centre of the ball is
View SolutionTwo smooth balls A and B , each of mass m and radius R , have their centres as shown in fig. Ball A , moving along positive x-axis, collides with ball B . Just before the collision, speed of ball 'A' is 4m//s and ball 'B' is stantionary. The collision What is velocity of ball 'B' after collision is
View SolutionTwo smooth balls and , each of mass and radius , have their centres as shown in fig. Ball , moving along positive x-axis, collides with ball . Just before the collision, speed of ball is and ball is stantionary. The collision
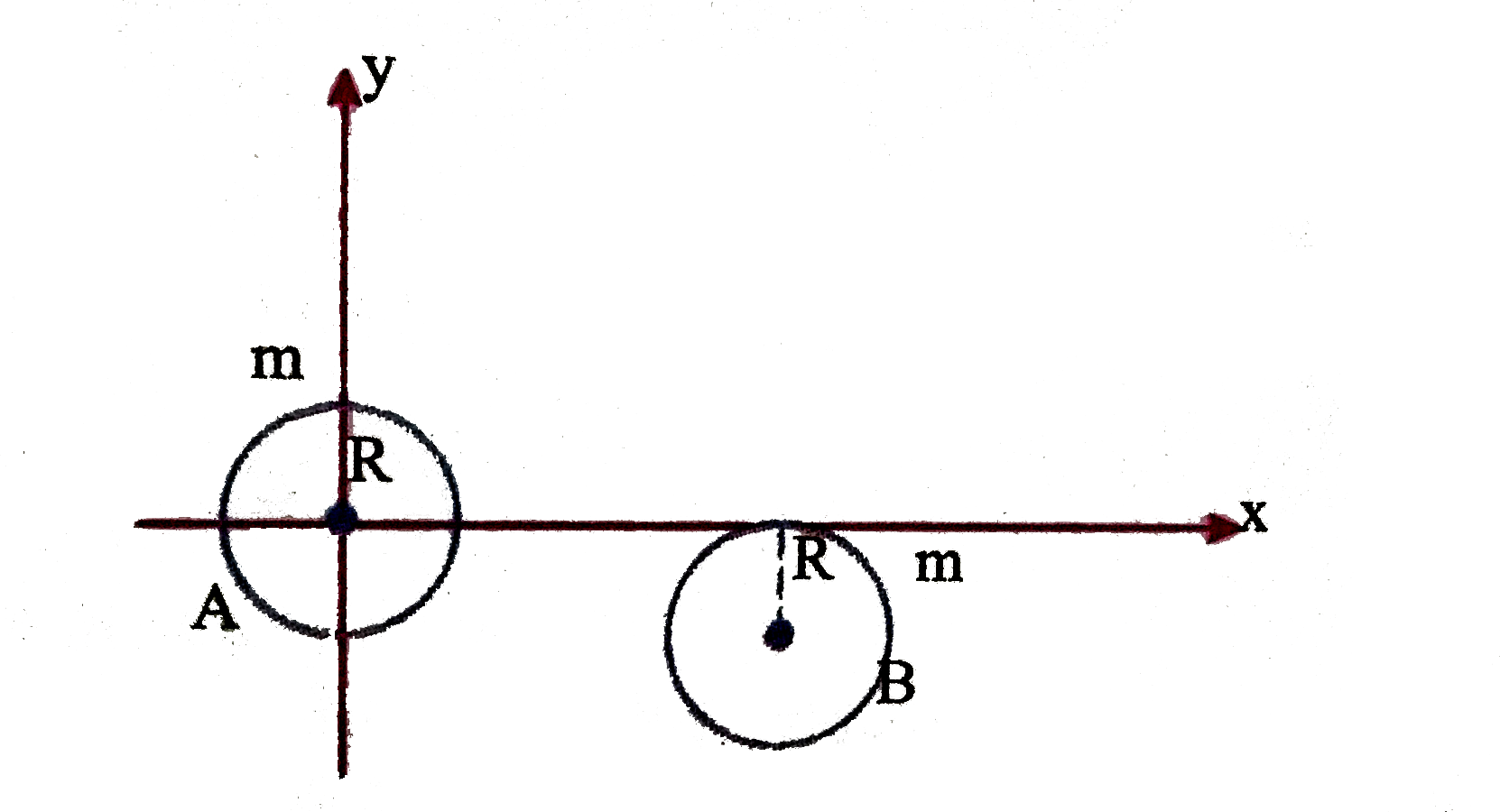
Velocity of the ball just after the collision is
View SolutionA tunnel is dug across the diameter of earth. A ball is released from the surface of Earth into the tunnel. The velocity of ball when it is at a distance from centre of earth is (where R = radius of Earth and M = mass of Earth)
View SolutionA tunnel is dug across the diameter of earth. A ball is released from the surface of Earth into the tunnel. The velocity of ball when it is at a distance from centre of earth is (where R = radius of Earth and M = mass of Earth)
View Solution