A rubber band of length l has a stone of mass m tied to its one end. It is whirled with speed v so that the stone describes a horizontal circular path. The tension T in the rubber band is - A zero B mv2 /l C > mv2/l D < mv2 /l
Correct option D < mv2 /lExplanation:
Related Solutions
A rubber band of length l has a stone of mass m tied to its one end. It is whirled with speed v so that the stone describes a horizontal circular path. The tension T in the rubber band is -
View SolutionA stone of mass m tied to a string of length l is rotating along a circular path with constant speed v. The torque on the stone is :
View SolutionA stone of mass 1 kg tied to a light inextensible string of length L = 10/3 m is whirling in a circular path of radius L in verticalplane . The ratio of maximum tension in the string to the minimum tension in the string is 4 and if g is taken to be 10 m//s^(2) . The speed of stone at the highest point of the circular path is
View SolutionTake a long rubber band and cut it at one point . At one of its ends tie a clean washed stone or a 50g weight as shown in figure Now hold the other end of the rubber band and make a mark there . Keep the stone hanging in air and measure the length of the rubber band from the stone to the mark made earlier . now take water in a pot and hold the rubber band at such a height that the stone sinks in it . again measure the length of the rubber band up to the mark . : What could be the reason for a shorter length of the rubber band in water ? :
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA stone of mass 1 kg tied to a light string of length m, is whirled in a vertical circle of radius L. If the ratio of maximum to minimum tensions is 4, the speed of the stone at the highest point of the circle is:
View SolutionA stone of mass 1 kg tied to a light string of length m, is whirled in a vertical circle of radius L. If the ratio of maximum to minimum tensions is 4, the speed of the stone at the highest point of the circle is:
View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View SolutionA stone of mass m is tied to a string of length l and rotated in a circle with a constant speed v . If the string is released, the stone flies
View SolutionA stone of mass m tied to a string of length l rotates along circumference of a circle with constant speed v. The torque on the stone is
View SolutionA stone of mass m is tied to a string of length L and rotated in a circle with a constant speed v, if the string is released the stone flies :
View SolutionTake a long rubber band and cut it at one point . At one of its ends tie a clean washed stone or a 50g weight as shown in figure
Now hold the other end of the rubber band and make a mark there . Keep the stone hanging in air and measure the length of the rubber band from the stone to the mark made earlier . now take water in a pot and hold the rubber band at such a height that the stone sinks in it . again measure the length of the rubber band up to the mark . :
What is observed ?: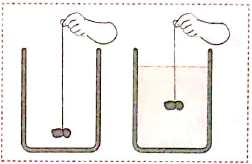
View SolutionA stone of mass m tied to a light inextensible sting of length L(=(10)/(3)m) is whirling in a circular path of radius L in a verticle plane. If the ratio of the maximum to the minimum tension is four, find the speed of the stone at the highest point of the circle.
View SolutionA stone of mass ied to a string of lengh l rotating along & a circular path with constant speed v. The torque on the stone is
View SolutionA stone of mass 1kg tied to a light inextensible string of length is whirling in a circular path of radius in vertical plane. If the ratio of the maximum tension in the string to the minimum tension in the string is 4 and if is taken to be , the speed of the stone at the highest point of the circle is.
View SolutionA stone of mass 1kg tied to a light inextensible sstring of length is whirling in a circular path of radius in vertical plane. If the ratio of the maximum tension in the string to the minimmum tension in the string is 4 and if is taken to be , the speed of the stone at the highest point of the circle is.
View SolutionA stone is tied to a string of length L and is whirled in a vertical circle,with the other end of the string at the centre. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of change in velocity as it reaches a horizontal position is
View Solution