In figure below suppose that the transmission axes of the left and right polarizing disks are perpendicular to each other also let center disk be rotated on the common axis with an angular speed ω . Show that if unpolarized light is incident on the left disk with intensity Imax of the beam emerging from right disk is I = 1/16 Imax 1 - cos 4ωt
For incident unpolarized light of intensity Imax :After transmitting 1st disk: I = 1/2 Imax After transmitting 2nd disk: I = 1/2 Imax cos2θAfter transmitting 3rd disk: I = 1/2 Imax cos2θ cos2 90° - θWhere the angle between the first and second disk is θ =ωt
Related Solutions
In figure suppose the transmission axes of the left and righit polarizing disks are perpendicular' to each other. Also, let the center disk be rotated on the common axis with an angular speed . That if unpolarized light is incident on the left disk with an intensity the intensity of the beam emerging from the right disk is given by . Find .
'(##CEN_KSR_PHY_JEE_C27_E01_038_Q08##)'
View SolutionAbout disks with equal inertial torque, about the axis perpendicular to the base of the disks through the center omega_(1) And omega_(2) Rotate with angular velocities of. If the axes of the two disks are aligned with each other, the expression for the energy loss during this event is
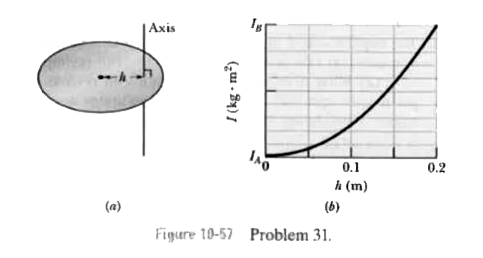
View SolutionFigure 10-57 a shows a disk that can rotate about an axis at a radial distance h from the center of the disk. Figure 10-57b gives the rotational inertia I of the disk about the axis as a function of that distance h, from the center out to the edge of the disk. The scale on the I axis is set by . What is the mass of the disk?
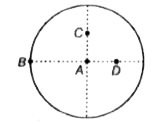
View Solutionकिसी एकसमान वृत्ताकार डिस्क ( चकती ) का जड़त्व आघूर्ण अधिकतम होगा, यदि घूर्णन अक्ष डिस्क के लम्बवत हो और वह गुजरती हो
View SolutionA rhinoceros beetle rides the rim of a small disk that rotates like a merry-go-round. If the beetle crawls toward the center of the disk, do the following (each relative to the central axis) increase, decrease, or remain the same for the beetle-disk system: (a) rotational inertia, (b) angular momentum, and ( c) angular speed?
View SolutionA thin circular disk of radius R is uniformly charged with density per unit area. The disk rotates about its axis with a uniform angular speed . The magnetic moment of the disk Is
View SolutionA thin circular disk of radius is uniformly charged with density per unit area.The disk rotates about its axis with a uniform angular speed .The magnetic moment of the disk is :
View SolutionA thin circular disk of radius is uniformly charged with density per unit area.The disk rotates about its axis with a uniform angular speed .The magnetic moment of the disk is :
View SolutionA circular disk of moment of inertia is rotating in a horizontal plane , about its symmetry axis , with a constant angular speed . Another disk of moment of inertia is dropped coaxially onto the rotating disk . Initially the second disk has zero angular speed . eventually both the disks rotate with a constant angular speed . The energy lost by the initially rotating disc to friction is
View Solutionजड़त्व आघूर्ण की एक वृत्ताकार डिस्क अपनी सममिति अक्ष के परितः, एक स्थिर कोणीय वेग से क्षैतिज तल में घूर्णन कर रही है। इस डिस्क के ऊपर जड़त्व आघूर्ण की एक अन्य डिस्क संकेन्द्री डाल दी जाती है। प्रारंभ में दूसरी डिस्क की कोणीय चाल शून्य है। अन्ततः दोनों डिस्क एक ही स्थिर कोणीय वेग से घूर्णन करने लगती हैं। प्रारंभ में घूर्णन करती हुई डिस्क की घर्षण के कारण नष्ट हुई ऊर्जा है ।
View SolutionDisk 1 rotates about a smooth vertical axis with the angular velocity omega_(1) . Disk 2 rotating with the angular velocity omega_(2) is kept on disk 1 while rotating in the same direction. Find the change in the rotational kinetic energy of the system given that the moments of inertia of the disks relative to the rotation axis are equal to I_(1)andI_(2) , respectively. The constant surface of the disks are rough.
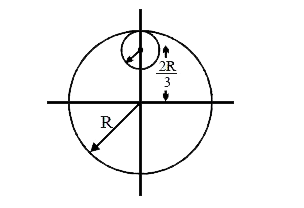
View SolutionR त्रिज्या तथा 9M द्रव्यमान के एकसमान गोलाकार डिस्क से त्रिज्या का एक छोटा गोलाकार डिस्क काट कर निकाल लिया जाता है, जैसा कि चित्र में दर्शाया गया है। डिस्क के सतह के लम्बवत् एवं उसके केन्द्र से गुजरने वाले अक्ष के सापेक्ष बची हुई डिस्क का जडत्व आघूर्ण होगा
View SolutionA solid disk rotates in the horizontal plane at an angular velocity of with respect to an axis perpendicular to the disk at its center. The moment of inertia of the disk is . From above, sand is dropped straight down onto this rotating disk, so that a thin uniform ring of sand is formed at a distance of 0.40 m from the axis. The sand in the ring has a mass of 0.50 kg. After all the sand is in place, what is the angular velocity of the disk?
View SolutionTwo disks are rotating about the same axis. Disk A has a moment of inertia of and an angular velocity of . Disk B is rotating with an angular velocity of . The two disks are then linked together without the aid of any external torques, so that they rotate as a single unit with an angular velocity of . The axis of rotation for this unit is the same as that for the separate disks. What is the moment of inertia of disk B?
View Solutionएक डिस्क के नियत कोणीय त्वरण इसके तल के लम्बवत् तथा इसके केन्द्र से गुजरने वाली अक्ष के परितः घूर्णन कर रही है। ज्ञात कीजिए
(a) 4 सेकण्ड पश्चात् डिस्क का कोणीय वेग तथा
(b) 4 सेकण्ड पश्चात् डिस्क का कोणीय विस्थापन।
View SolutionA flat uniform circular disk (radius = 2.00 m, kg) is initially stationary. The disk is free to rotate in the horizontal plane about a frictionless axis perpendic ular to the center of the disk. A 40.0-kg person, standing 1.25 m from the axis, begins to run on the disk in a circular path and has a tangential speed of relative to the ground. Find the resulting angular speed of the disk (in ) and describe the direction of the rotation.
View Solution6 सेमी की डिस्क में से 1 सेमी त्रिज्या का एक छिद़ काट दिया जाता हैं छिद्र का केंद्र डिस्क के केंद्र से 3 सेमी की दूरी पर है शेष डिस्क के द्रव्यमान केंद्र की स्थिति होगी
View SolutionA circular disk of moment of inertia I_t is rotating in a horizontal plane, about its symmetry axis,with a constant angular, speed omega_1 Another disk of moment of inertia I_b is dropped coaxially onto the rotating disk initially the second disk has zero angular speed.Eventually both the disks rotate with a constant angular speed omega_f The energy lost by the initially rotating disc to friction is :
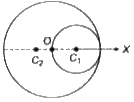
View Solutionत्रिज्या R की एक समान वृत्ताकार डिस्क से त्रिज्या R/4 की एक समाक्ष छोटी वृत्ताकार डिस्क काट ली गई है। यदि सम्पूर्ण डिस्क का केंद्र O हो तो शेष डिस्क के द्रव्यमान केंद्र की O से दूरी होगी
View SolutionA unifrom solid disk of radius and mass is free to rotate on a frictionless pivot through a point on its rim. If the disk is released from rest in the position shown in figure. The speed of the lowest point on the disk in the dashed position is.
 .
.
View Solution