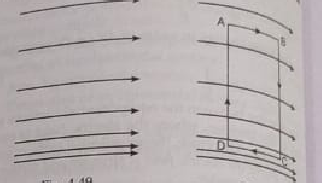
Using the solution of the preceding problem show that it is impossible to create an electric field in which all the lines of force are parallel lines whose density increases continuously in a direction perpendicular to the lines of force Fig..
For the proof it is necessary to calculate the work done by the electric forces for a displacement of a charge q over the closed rectangular contour ABCD Fig.. Since the lines of force are parallel the field intensity E along each of the lines of force is constant. Since the lines of force on side AB are less dense than on side CD the field intensity E1 and therefore also the work A1 in displacing a charge along AB will be less than the field intensity E2 and the work A2 along side CD. The work done in displacing the charge along BC and DA is zero since the vector E is perpendicular to the direction of motion of the charge. Consequently the work done over the entire closed path ABCD is equal to A1 — A2 which is different from zero.Since in an electrostatic field the work done by the electric forces over any closed path is always equal to zero the result we have just obtained is in contradiction to this fundamental property of electrostatic fields and the conditions stated in the problem cannot exist.
Related Solutions
Can we create an electric field in which all the lines of force are parallel but their density increases continusously in a direction per-pendicular to the lines of force, fig. ,
View SolutionWork done to move a charge along a closed path inside an electric field is always zero. Use this fact to prove that it is impossible to produce an electric field in which all the lines of force would be parallel straight lines and the density of their distribution would constantly increase in a direction perpendicular to the lines of force as shown in Figure.
View Solutionएक आविष्ट कण विद्युतीय क्षेत्र में स्वतन्त्र रूप से गति में है। यह
(a) बल रेखा के लम्बवत गतिशील होगा
(b) बल रेखा के समानान्तर गतिशील होगा
(c ) किसी भी दिशा में गतिशील हो सकता है
View SolutionWhich of the following is correct regarding electric lines of force ?
(i) Electric lines of force diverge from and converge at a charge
(ii) Electric lines of force never cross each other , otherwise there will be two directions of electric field at a point of intersection which is not possible
(iii) Closer are the electric lines of forces , stronger is the field , and further apart lines of force ,weaker is electric field
(iv) The electric lines of forces are parallel for a uniform electric field
View SolutionRepresent a uniform electric field using lines of force.
View SolutionThe property of the electric line of force (a) The tangent to the line of force at any point is parallel to the direction of .E. at that point (b) No two lines of force intersect each other
View SolutionThe property of the electric line of force (a) The tangent to the line of force at any point is parallel to the direction of .E. at that point (b) No two lines of force intersect each other
View SolutionThe property of the electric line of force a. Electric lines of force are just imaginary lines b. Electric lines of force will be parallel to the surface of conductor c. If the lines of force are crowded, them field is strong d. Electric lines of force are closed loops
View SolutionAssertion: Direction of electric field is tangent to the line of force
Reason: A charge will always travel along the lines of force.
View SolutionAn electron enters an electric field with its velocity in the direction of the electric lines of force. Then
View SolutionAnswer each bit as directed: Electric lines of force represent ______ of electric field.
View SolutionAn electron enters in an electric field with its velocity in the direction of the electric lines of force. Then
View SolutionAn electron enters an electric field with its velocity in the direction of the electric lines of force. Then
View SolutionAn electron enters an electric field with its velocity in the direction of the electric lines of force. Then
View SolutionAnswer each bit as directed:
Electric lines of force represent ______ of electric field.
View SolutionFig shows electric lines of force emerging from a charged body. Is electric field intensity more at A or B?
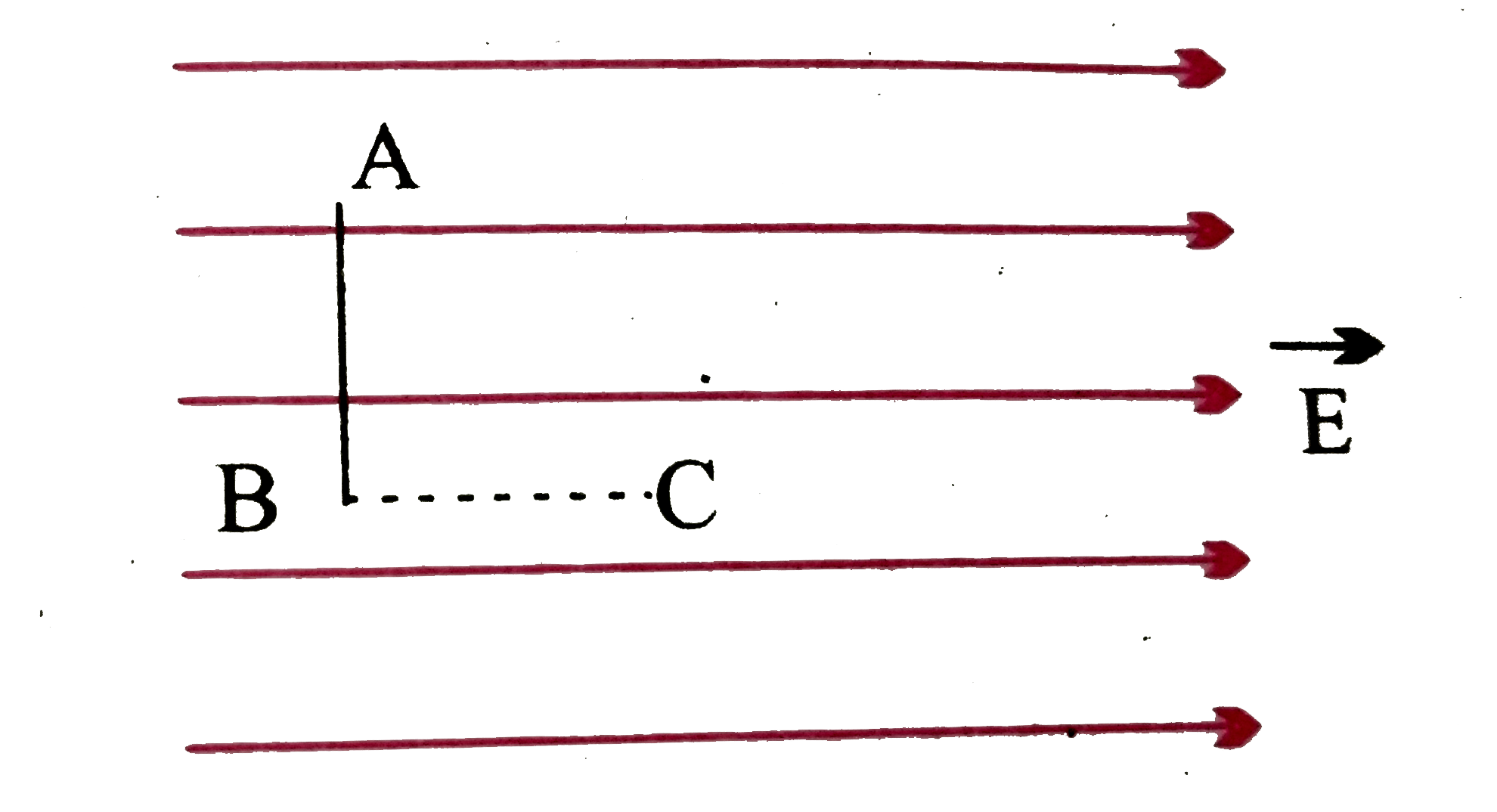
View Solutionएकसमान विद्युत-क्षेत्र E में तीन बिन्दु A , B और C प्रदर्शित किये गये है | रेखा AB बल रेखाओ के लम्बवत तथा BC समान्तर है | तब निम्न में से कौन-सा कथन सत्य है -
View SolutionWhich of the following statements are correct.
(a) Electric lines of force are just imaginary lines
(b) Electric lines of force will be parallel to the surface of conductor
(c ) If the lines of force are crowded, then field is strong
(d) Electric lines of force are closed loops
View SolutionWhich of the following statements are correct?
a. Electric lines of force are just imaginary lines
b. Electric lines of force will be parallel to the surface of conductor.
c. If the lines of force are crowded, them field is strong
d. Electric lines of force are closed loops
View SolutionWhich of the following statements are correct, a) Electric lines of force are just imaginary lines b) Electric lines of force will be parallel to the surface of conductor c) If the lines of force are crowded then field is strong d) Electric lines of force are closed loops
View Solution