Two particles are moving with relativistic velocities in directions at right angles they have momenta p1 and p2 and total energies E1 and E2. If they are the sole products of disintegration of a heavier object what was the rest mass velocity and direction of motion?
M0βγ = p1sinθ + p2cosθ momentum conservation along x-axis 1 p1cosθ = p2sinθ momentum conservation along y-axis 2 M0γ = E1 + E2 Energy conservation 3
Related Solutions
A particle moving with a velocity equal to is subjected to an acceleration of for 2 seconds in a direction at right angles to the direction of motion. The magnitude of the final velocity is
View SolutionA particle moving with a velocity equal to 0.4ms^(-1) is subjected to an acceleration of 0.15ms^(-2) for 2 seconds in a direction at right angles to the direction of motion. The magnitude of the final velocity is
View SolutionTwo relativistic particles move at right angles to each other in a laboratory frame of reference, one with the velocity v_1 and the other with the velocity v_2 . Find their relative velocity.
View SolutionA particle of mass m moving with velocity u collides elastically head on with a particle of mass 2m at rest. After collision the heavier particle moves with velocity?
View SolutionA particle of mass m moving with velocity u collides elastically with a particle of mass 3m at rest. After collision the heavier particle moves with velocity.
View SolutionA particle of mass m moving with velocity u collides elastically with a particle of mass 3m at rest. After collision the heavier particle moves with velocity
View SolutionAssertion : A lighter object and a heavier object having equal momenta, also have equal kinetic energies. Reason : Kinetic energy varies inversely as the square of velocity.
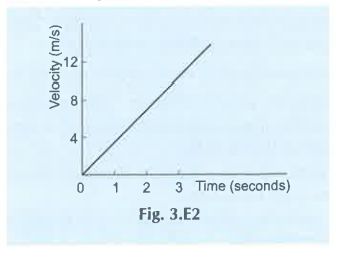
View SolutionFigure 3.E2 shows the velocity -time graph for a particle moving in a fixed direction. Find the acceleration of the particle.
View Solutionসমদ্রুতিতে বৃত্তপথে ঘূর্ণায়মান কণার বেগের অভিমুখ কীরূপ হয়?
View SolutionAssertion : An object may have acceleration even if it is moving with uniform velocity Reason : An object may be moving with uniform velocity but it may be changing its direction of motion
View SolutionA particle of rest mass m', velocity V=(4c)/(5) Find the kinetic energy and total energy of the particle that is moving with
View SolutionA particle of mass m1 is moving with a velocity and another particle of mass is moving with a velocity v2. Both of them have the same momentum but their different kinetic energies are E1 and E2 respectively. If then
View SolutionA particle of mass m1 is moving with a velocity v_(1) and another particle of mass m_(2) is moving with a velocity v2. Both of them have the same momentum but their different kinetic energies are E1 and E2 respectively. If m_(1) gt m_(2) then
View SolutionIf a particle is at rest with three velocities of 14 units, 16 units and 26 units on it, then the angle between the directions of the two smaller velocities is :
View SolutionA particle moving with a velocity equal to is subjected to an acceleration of for . in a direction at the right angle to its direction of motion. The resultant velocity is
View SolutionA particle moving with a velocity equal to is subjected to an acceleration of for 2 seconds in a direction at right angles to the direction of motion . The magnitude of the final velocity is
View SolutionA particle moving with a velocity equal to is subjected to an acceleration of for 2 seconds in a direction at right angles to the direction of motion. The magnitude of the final velocity is
View SolutionA particle moving with a velocity equal to is subjected to an acceleration of for 2 seconds in a direction at right angles to the direction of motion . The magnitude of the final velocity is
View SolutionA particle moving with a velocity equal to 0.4 ms^(-1) is subjected to an acceleration 0.15ms^(-2) of for 2 seconds in a direction at right angles to the direction of motion. The magnitude of the final velocity is
View SolutionA particle moving with a velocity equal to 0.4ms^(-1) is subjected to an acceleration of 0.15 ms^(-2) for 2 seconds in a direction at right angles to the direction of motion. The magnitude of the final velocity is
View Solution