In a Young double slit experiment the aperture screen distance is 2 m. The fringe width is 1 mm. Light of 600 nm is used. If a thin plate of glass μ =1.5 of thickness 0.06 mm is placed over one of the slits then there will be a lateral displacement of the fringes by: a 0 cmb 5 cmc 10 cmd 15 cm
Correct option b 5 cmExplanation:When a glass plate of width t and refractive index µ is kept in path of one ray say S2P then the fringe shift n is given as
Related Solutions
In Young's double slit experiment, the aperture screen distance is 2 m. The fringe width 1 mm light of 600 nm is used. If a thin plate of glass ( = 1.5) of thickness 0.06 mm is placed over one of the slits, the there will be a lateral displacement of the fringe by
View SolutionIn Young's double slit experiment, the aperture screen distance is . The fringe width is . Light of is used. If a thin plate of glass of thickness is placed over one of the slits, then there will be a lateral displacement of the fringes by
View SolutionIn Young's double slit experiment, the aperture screen distance is 2m . The fringe width is 1mm . Light of 600nm is used. If a thin plate of glass (mu=1.5) of thickness 0.06mm is placed over one of the slits, then there will be a lateral displacement of the fringes by
View SolutionIn a Young’s double slit experiment, the distance of screen from slits is 2 m. The fringe width is 0.5 mm. If a thin glass plate of thickness 0.05 mm and n = 1.5 is placed over one of the slits, then the lateral displacement of fringes will be (lambda= 6000 overset@A)
View SolutionIn Young's double slit experiment the fringe width is found to be 0.3 mm. Now if a thin glass plate of refracting index 1.5 is placed in the path of any one of light rays coming from the slits then the width of the fringe will be
View SolutionYoung’s double slit experiment gives interference fringes of width 0.3 mm. A thin glass plate made of material of R.I. 1.5 is kept in the path of light from one of slits, then the fringe width become :
View SolutionIn Young's double slit experiment, the distance between the two slits is and the wavelength of light used is . If the width of the fringe on the screen is 4 mm , the distance between screen and slit is
View SolutionIn a double experiment, the distance between the slit is 1 mm and screen is 25 cm away from the slits. The wavelength of light is . The width of the fringe on the screen is
View SolutionIn Young's double slit experiment the distance of the screen from the plane of the slits is 1.0 m. The wavelength of light used and width of the fringe are 6000 Å and 2 mm respectively.
If the wavelength of the light used is 4800 Å, the width of the fringe will be
View SolutionIn Young's double slit experiment, the distance between the two slits is 0.1 mm, the distance between the screen and the slit is 100 cm. if the width of the fringe is 5 mm, then the wavelength of monochromatic light used is
View SolutionIn a experiment, the distance between the slits the screen is . For a certain distance between the slits, an interference pattern is observed on the screen with the fringe width . When the distance between the slits is increased by the fringe width decreased to of the original value. In the final position, a thin glass plate of refractive index is kept in front of one of the slits the shift of central maximum is observed to be fringe width. Find the thickness of the plate wavelength of the incident light.
View SolutionIn a YDSE experiment, the distance between the slits & the screen is 100 cm . For a certain distance between the slits, an interference pattern is observed on the screen with the fringe width 0.25 mm . When the distance between the slits is increased by Deltad=1.2 mm, the fringe width decreased to n=2//3 of the original value. In the final position, a thin glass plate of refractive index 1.5 is kept in front of one of the slits & the shift of central maximum is observed to be 20 fringe width. Find the thickness of the plate & wavelength of the incident light.
View SolutionIn Young's double slit experiment, the distance between two slits is 0.1 mm. If the screen is placed at a distance of 1.0 m from the slits and the wavelength of light 5000 Å , then the fringe width is:
View SolutionIn Young's double slit experiment, the distance between the slits is 1 mm and that between slit and screen is 1 meter and 10th fringe is 5 mm away from the central bright fringe, then wavelength of light used will be
View SolutionIn a standard Young's double-slit experiment with coherent light of wavelength 600 nm, the fringe width of the fringes in the central region (near the central fringe, ) is observed it to be 3 mm. An extremely thin glass plate is introduced to be displaced by 11 mm. Another thin plate is placed before the second slit and it is observed that the fringe are now displaced by an additional 12 mm. If the additional optical path lengths introduced are and then
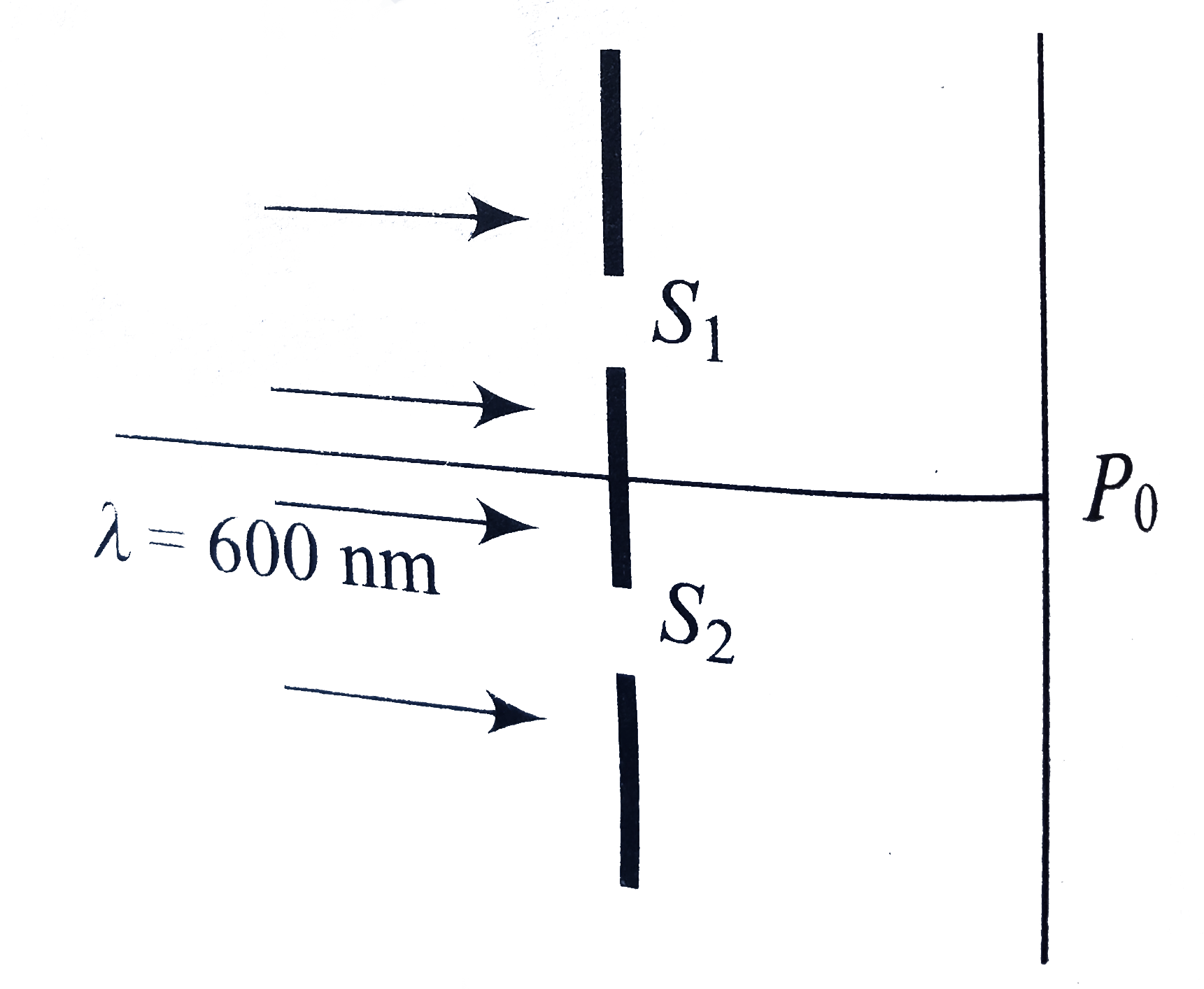
View SolutionIn a standard Young's double-slit experiment with coherent light of wavelength 600 nm, the fringe width of the fringes in the central region (near the central fringe, P_(0) ) is observed it to be 3 mm. An extremely thin glass plate is introduced to be displaced by 11 mm. Another thin plate is placed before the second slit and it is observed that the fringe are now displaced by an additional 12 mm. If the additional optical path lengths introduced are Delta_(1) and Delta_(2) then
View SolutionIn Young's double-slit experiment the distance between the slits is 1 mm and that between slit and screen is 1m. If 10th bright fringe is 5 mm away from the central bright fringe, then wavelength of light used will be
View SolutionIn a Young's double slit experiment the spacing between the slits is 0.3mm and the screen is kept at a distance of 1.5m . The second bright fringe is found to be displaced by 6 mm from the central fringe. The wavelength of the light (in nm ) used in the experiment is
View SolutionThe separation between the. consecutive dark fringes in a Young's double slit experiment is 1 mm. The screen is placed at a distance of 2.5 m from the slits and separation between the slits is 1.0 mm. Calculate the wavelength of light used for the experiment.
View SolutionIn YDSE, separation between slits is 0.15 mm, distance between slits and screen is 1.5 m and wavelength of light is 589 nm, then fringe width is
View Solution