If u is the energy density of radiation then show that the radiation pressure is given by Prad = u/3.
Using the analogy between radiation photon gas and gas molecules the photons move in a cavity at random in all directions rebounding elastically from the walls of the cavity. The pressure exerted by an ideal photon gas isp = 1/3ρ where ρ is the mass density. In the case of photon gas the speed of all photons is identical being equal to c. Furthermore from Einstein’s relationu = ρc2where u is the energy density. Replacing by c2prad = 1/3ρc2 = u/3
Related Solutions
What is radiation pressure ? Mention its relation with density of radiated energy .
View SolutionFind the temperature of totally ionized hydrogen plasma of density at which the thermal radiation pressure is equal to the gas kinetic pressure of the particles of plasma. Take into account that the thermal radiation pressure , where is the space density of radiation enegry, and at high temperatures all substances obey the equation of state of an ideal gas.
View SolutionShow that the energy density of em radiation is . Hence, find the intensity of radiations?
View SolutionThe energy density of an ideal gas is related to its pressure P as
View SolutionThe energy density u/V of an ideal gas is related to its pressure P as
View SolutionWhat is the relation between pressure p of a gas and its energy density u?
View SolutionThe temperature of a spherical shell of radius R is T. The black mass radiation inside it can be considered as an ideal photon gas with u energy per unit volume (u = U / V prop T ^ 4) with a pressure of 1/3 (U / V). Now the relation of T and R will be when the heat of the creator expands
View Solution""_(92)U^(238) decays successively to form ""_(92)U^(234) . What are the radiations emitted in these three steps?
View Solutiondecays successively to form . What are the radiations emitted in these three steps.
View SolutionIf radiation is totally absorbed and energy incident on surface in time t be U then write equation of momentum imparted to surface.
View SolutionObtain the maximum kinetic energy of -particles, and the radiation frequencies of decays in the decay scheme shown in Fig. . You are given that
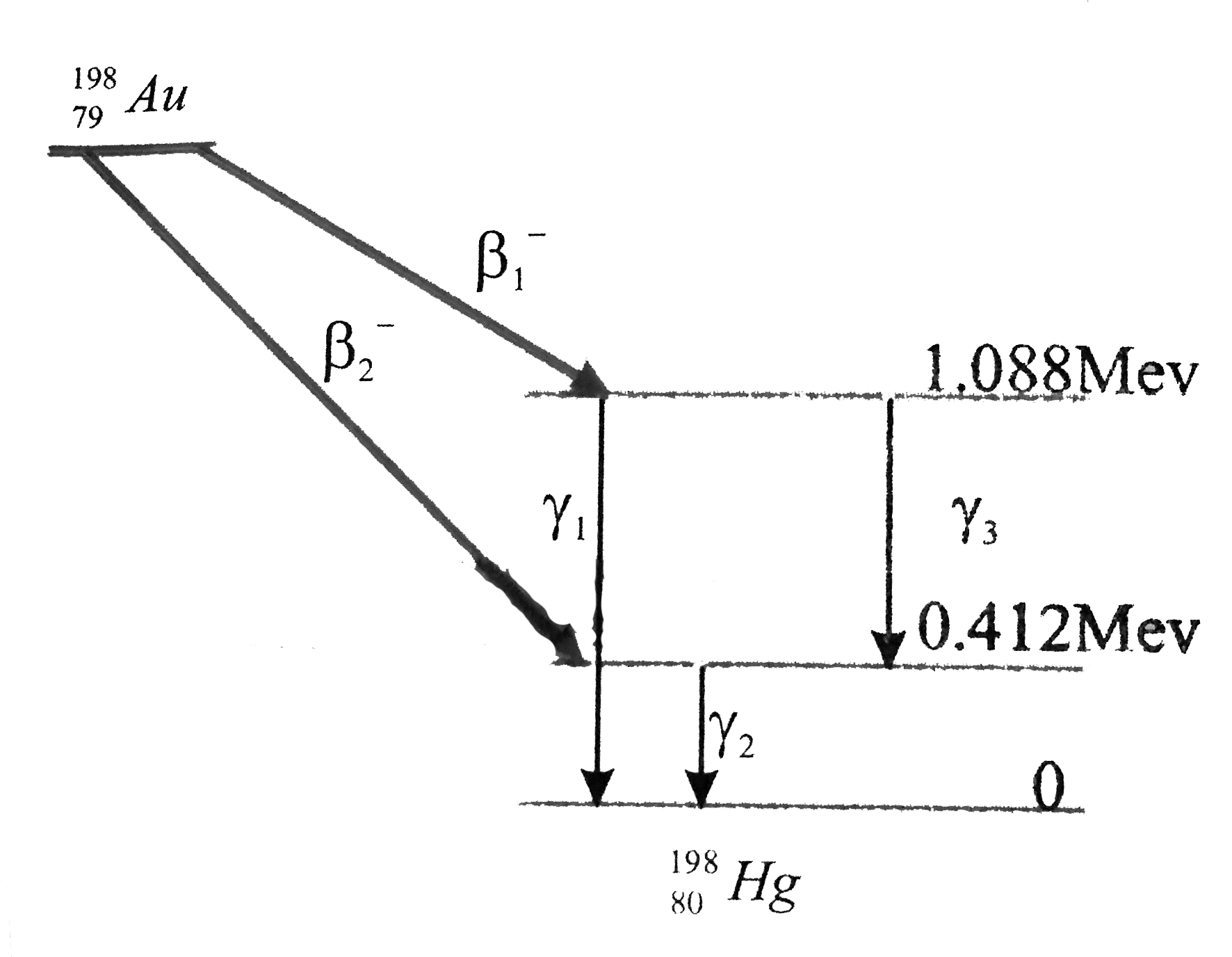
View SolutionObtain the maximum kinetic energy of - particle and the radiation frequencies corresponding to decays in the figure given below. (rest mass of au -198.968233 u and r.m. of Hg=198=197.966760 u)
View SolutionObtain the maximum kinetic energy of b-particles, and the radiation frequencies of g decays in the decay scheme shown in Fig. You are given that m(""_(8)^(19)Au) = 197.968233 u m(""_(8)^(19)Hg) =197.966760 u .
View SolutionObtain the maximum kinetic energy of beta -particles, and the radiation frequencies of gamma decays in the decay scheme shown in Fig. 13.6. You are given that m( "^198Au ) = 197.968233 u m( "^198Hg ) =197.966760 u :
View SolutionObtain the maximum kinetic energy of beta -particles, and the radiation frequencies of gamma decays in the decay scheme shown in Fig. 14.6 . You are given that m(.^(198)Au)=197.968233 u, m(.^(198)Hg)=197.966760 u
View SolutionA black body at a high temperature T radiates energy at the rate of U (in Wm^(-2) ). When the temperature falls to half (I e . (T)/(2) ) the radiated energy (in Wm^(-2) ) will be
View SolutionRadiation Pressure
View SolutionRadiation Pressure
View SolutionRADIATION PRESSURE
View SolutionRadiation pressure on any surface (for given intensity):
View Solution